Sheri Rowe

Sheri Rowe is an elementary teacher and guidance counselor in Sarnia, ON. She is also a graduate student at Western University in the MPEd mathematics program.

What should one expect when they begin down that journey of teaching their students computational thinking skills?  From my experience, the path is neither linear nor like sailing on a calm lake.  It is, however, a journey worth taking as it has many surprises and positive impacts on student learning and engagement.  This report summarizes my observations, reflections and questions that arose as I explored different technologies that would develop computational thinking in my intermediate students.

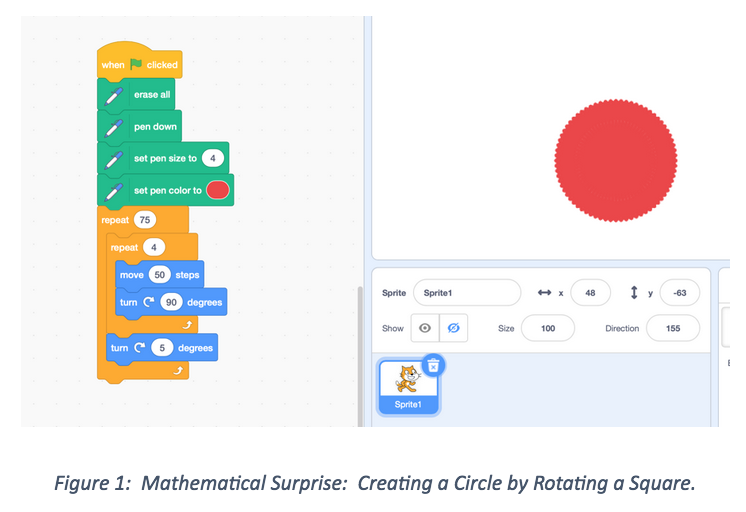
It doesn’t matter whether the first computational thinking assignment involved a programmable robot, a micro:bit or an online coding program like Scratch, there was always a group of students who felt frustrated or confused and told me that they could not do this because they did not know what they were doing.  The overwhelming number of negative comments made me want to give up and return to a traditional lesson where I taught the concept, but then I noticed that there was another group of students that were engaged and welcomed the change of pace and the challenge.  What was more surprising was that some of the students absorbed in the assignment would not typically be engaged in math activities.  Each time I introduced programming to a new class, I decided to stay the course and give my students time to play with the technology to see what they could create.  It didn’t take long before someone in the class shared their success with much excitement.  Other students immediately gathered around to witness the small success and were now motivated to do it themselves.  They began to ask questions of their peers and the classroom was a buzz of conversation, discoveries and more excitement.  Some students took my open assignment in their own direction and went beyond the original assignment to possibly discover a higher-level math concept, like rotating a shape repeatedly to create a circle.   Some of their programs looked different than my attempts, but that was okay because they had created a program that made sense to them.  Other students saw what their classmates had created and returned to their programs to attempt to make them better.  Once the students understood the basic idea of block programming, coding met them where they were at.  It was exciting when they were able to edit the program to create a triangle, but it was just as exciting to see them conceptualize a new idea, break it down into smaller steps and create a square and a triangle on the same stage or create a pattern of shapes with various colours, rotations, and sizes.  That is the beauty of coding, it provides a differentiated learning experience where all students can succeed.  That being said, there were still students who wanted to give up because the program wouldn’t run.  On the surface, it appeared that these students had not learned to persevere through difficult situations or had a negative attitude about STEM, but after a conversation, the reality was that these students had not developed the skill of troubleshooting.  It made me wonder if this was the same issue that arises when they are solving math problems.  Are they lacking in strategies that can help them to get unstuck?

What I love about this type of assignment is that I have an opportunity to be the student and the teacher.  My students are on a level playing field with me.  We learn from one another and celebrate our successes together.  They get to witness my thinking processes and I theirs.  I also love that I have an opportunity to learn more about their interests and unique personalities through the conversations that occur in this more relaxed setting or from the personalized products they create.  In this collaborative setting, students are more willing to share their thoughts and curiosities.  After my most recent activities involving Scratch, my students started to wonder about how hard it would be to program in another language like Python, how can we get a larger stage, or could we code a game?  Another student commented that when he codes, he feels like he has power because he can create what he wants.  Coding seems to foster a curiosity unlike any other making activities I have tried and the self-directed nature of it lets them explore and create what they want.

The excitement from computational thinking activities does not stay confined to my classroom.  It has as Gadanidis (2016) would say, wide walls.  Students talk in the halls about their programs with students from other classes, parents comment on how they saw or heard about their child’s creation and I, the teacher, cannot keep the experience to myself.  I share my stories and materials with other colleagues in hopes that they will join me in my adventure.

What I notice with coding is that the first session is the most challenging as a teacher.  They are new to the computational thinking experience and as one of my students said, “this is not like anything I have ever done before.”  Even when given a Scratch code to use and edit, some students were unable to move the sprite without guidance; however, by the second session where they were coding a joke or a scene from a movie or TV show, they were able to intuitively move the sprite on the stage without having knowledge of the cartesian coordinate system.  The intuitive nature of coding is what makes it a low-floor, high-ceiling activity.   Students do not need formal lessons on the math concepts prior to coding.  I would not have believed it until I saw it with my own eyes.  I had concerns that my students would not be able to determine the angle of rotation because they had not been taught the geometry concepts.  My knowledge of Euclidean geometry did not allow me to see that there was another way to find the rotation angle when creating shapes.  The idea of using my body to act out the commands for the sprite was foreign to me, but surprisingly easy to understand.  It made me wonder how many other concepts could be simplified if I would look at the concept through a lens other than Euclidean geometry.  Another interesting observation that challenged my pedagogy was that a day after our second coding session, I taught a lesson on the coordinate system and used the sprite in the scratch program as a tool to help them understand the grid.  Some students immediately went back to modify their programs rather than completing the assigned practice questions.  This made me wonder if the practice questions were necessary and if my practice assignment should have been to return to a coding assignment and apply their new knowledge.  By applying their knowledge to something that they are invested in and have an emotional attachment to may help “deepen the learning of mathematical and science content” (Weintrop, Beheshti, Horn, Orton, Jona, Trouille, Wilensky, 2016) which is what I hope to achieve.  This new insight has me rethinking some of my practice activities.

Overall, my experiences with coding in the intermediate classroom have been positive.  I feel that I have a powerful tool that has been added to my teacher toolbox.  By embedding coding into my classroom, students have an opportunity to not only make sense of the math they are learning when they apply it in their program but also are given an activity that allows them to practice computational thinking skills like conceptualizing the problem, breaking the problem down into smaller steps, troubleshooting and refining.  On top of that, coding also provides my students with access to higher-level concepts and engages students that may not normally perform well on standard assessments.  The low floor, high ceiling and wide wall nature allows all students to participate at a level that is engaging for them, and as a result, their enthusiasm spills over to other people when they share their creations and new insight.  For me, the look on their face and the excitement in their voice makes me the happiest teacher in the world and reminds me why this was a journey worth taking.

Sheri Rowe

Feb 13, 2021

References:

• Gadanidis, G., Hughes, J. M., Minniti, L., & White, B. J. G. (2016). Computational thinking, grade 1 students and the binomial theorem.  Digital Experiences in Mathematics Education, 3, 77-96.
• Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2015). Defining computational thinking for mathematics and science classrooms.  Journal of Science Education and Technology, 25(1), 127-147.