Immaculate K. Namukasa
The past few months have marked several Computational Thinking and Coding events including the Canadian CT and mathematics education Symposium http://ctmath.ca/computational-thinking-in-mathematics-education-symposium/, the International Hour of Code https://hourofcode.com/ca , as well as the International Conference on Computational Thinking Education https://www.eduhk.hk/cte2017/. Several students in classrooms are tinkering, thinking and creating with computational thinking activities including programming, modelling and design thinking activities.
A big question in computational thinking activities remains: How do educators categorize the computational thinking and coding activities which they are offering to their students? One way to categorize the learning opportunities that arise from computational thinking, per Sengupta et al., (2013) is: Introductory, Intermediate and Advanced. At each of these levels, students engage in computational thinking activities in which domain-specific concepts, such as mathematics concepts, are enacted, practiced or consolidated.
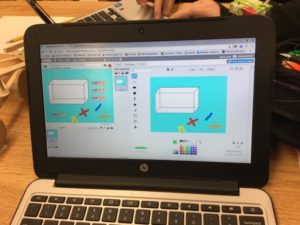
Introductory Computational Thinking Activities: Introductory activities include activities in which the students are introduced to a CT context (such as coding, digital making or designing), its basic concepts (e.g., coding concepts such as sequencing and loops) and/or a specific tool (e.g., a block-based programing language such as scratch). The blank-create model (NRC, 2011) may be used for the introductory level activities where students explore the tools following guided instructions and an overall set goal (e.g., to program a character or robot to move in or to draw geometry shapes). Next, a prompt is provided for students to challenge themselves to work on the next task or to create a project. I have found that it is always important to have a content-centred learning goal even when students are simply exploring the tool. Figure 1 shows an exploration center on coding the Cubetto robot to move from one part of the city to another on its map (e.g., from the castle to the bank). Students engage in this activity using a limited amount of motion commands (e.g., forward, backward, right turn, left turn, repeat) and the function command (a blue block used to represent several assembled commands) available in the kit. Students soon learn to use the function block to group repeated commands (e.g., move backward, right turn and repeat).
My experience is that elementary school students (Grade 4 and younger), need to engage in introductory activities with at least one computational thinking context or tool before they meaningfully engaged in intermediate activities with the same or another CT context or tool. Introductory activities, for example, introduce students to the basic concepts such as assembling code in a sequence and the idea of an algorithm assemble to command a character on screen or a robot as well as using repeat loops, and some logic.
concepts such as assembling code in a sequence and the idea of an algorithm assemble to command a character on screen or a robot as well as using repeat loops, and some logic.
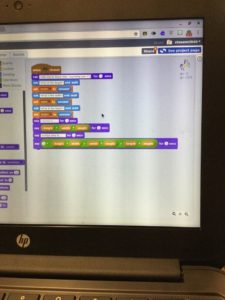
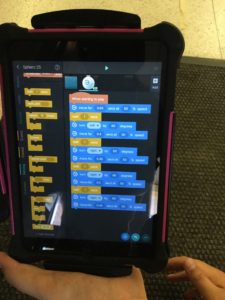
Intermediate Computational Thinking Activities: Intermediate activities may involve using a specific computational thinking tool to complete a challenge (e.g., programming a robot to navigate a maze or terrain marked on the floor) or to design and work on a project (e.g., design a project on a screen-based tool) or to complete an advanced level of a computational thinking app or game. During intermediate activities, the use-modify-create model (Grover & Pea, 2012; NRC, 2011) can help learners modify examples shared with them to achieve specific projects. This ability to modify examples could also demonstrate learning and improvement in computational thinking as students use increasingly elegant, efficient, and sophisticated approaches to tackle computational thinking explorations (NRC, 2011). Figures 2 to 5 show examples of intermediate projects with Scratch and with the Sphero Robot, each with their corresponding code.
Advanced Computational Thinking Activities: Students may be prompted to engage on advanced tasks in which coding is used as a tool (e.g., in designing a math interface or a student-made app representing a mathematics solution, pattern or formulae). Text-based programming languages such as Python (Bird et al., 2014) and digital programmable materials, such as wearables, are examples of advanced computational thinking activities. Activities with these tools are ideal for when students are transitioning from intermediate activities or when they have an opportunity to engage in computational thinking activities over several sessions.
Concepts Enacted by CT tools: In the examples shared above, mathematics is the domain-specific context in which characters, robots, or students perform concepts such as geometry concepts (e.g., moving in a defined path, drawing or stamping geometrical shapes), and measurement concepts (e.g., of linear, area and volume measurements and formulae). Other contexts are possible, such as number concepts (e.g., coding math machines that perform calculation such as making change, multiplication facts) and patterns (e.g., coding repeating patterns).
This issue features 4 articles: The Where Art and Math is greater than Math plus Art article about a number patterning context in which students modify the given code to generate different number patterns. The article on Computational Thinking and Design Thinking is about a variety of contexts in which a teacher may engage students in computational thinking activities throughout the year. The article Edison blocks explores a specific robot, the Edison block robots, with younger students. Lastly, End of year math, is about engaging students in Scratch computational thinking activities during the end of the year when they are reviewing their mathematics curriculum.
References:
Sengupta, P., Kinnebrew, J. S., Basu, S., Biswas, G., & Clark, D. (2013). Integrating computational thinking with K-12 science education using agent-based computation: A theoretical framework. Education and Information Technologies, 18(2), 351-380.
National Research Council, NRC. (2011). Committee for the Workshops on Computational Thinking: Report of a workshop of pedagogical aspects of computational thinking. Washington, DC: National Academies.
Grover, S., & Pea, R. (2013). Computational thinking in K-12: A review of the state of the field. Educational Researcher, 42(1), 38-43.
Bird, J., Caldwell, H., & Mayne, P. (2014). Lessons in teaching computing in the primary schools. Los Angeles: Sage.
Kafai, Y. B. (2015). Connected code: A new agenda for K-12 programming in classrooms, clubs, and communities. Paper presented at the Math + Coding Symposium, Western University, London, Ontario, Canada.
Immaculate Kizito Namukasa is an associate professor of education at Western University in Ontario and distinguished as a teaching fellow with the teaching support center at Western University, 2017 to 2020 based on her work on pedagogies incorporating maker activities in teaching. She is a past journal editor for the Ontario Mathematics Gazette – a magazine for teachers and educators and a current editor Math + code ‘Zine. For more information see http://bit.ly/IKNamukasaWesternEducation.