by Namukasa, Kizito Immaculate, Western University; Patel, Minakshi, Thames Valley District School Board; Miller, Marja, Western University
Integrating computational thinking (CT) in teaching specific K-12 school curricular is a more recent development than teaching CT in university and college courses. In this article, we share some insights on teaching practices that support integrating introductory computational thinking activities with school curricular activities for middle grades students. We specifically reflect on the tools and materials to use when integrating computational thinking concepts and mathematics curricular concepts in grade 4-8 classrooms. In this paper, we refer to integration of computational thinking concepts and mathematics curricular concepts as CT and mathematics.
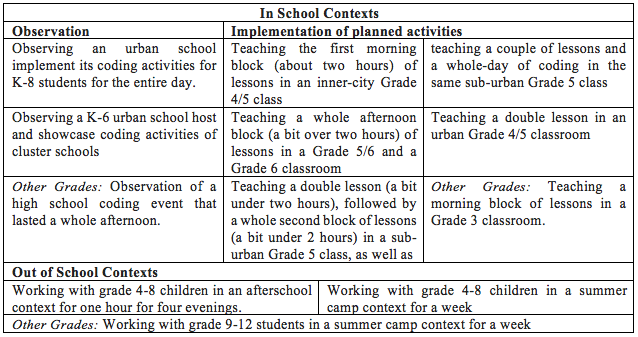
This past year we had the opportunity to design, implement and observe CT and mathematics activities in school and out of school contexts. We share the specific contexts of the project we carried out in Table 1. Most examples we use as illustrations are from a sub-urban Grade 5 class in Ontario in which we implemented several CT and mathematics activities. We designed several activities on mathematics topics including measurement, patterning and geometry. Some of the activities we designed were embedded within a lesson, a set of lessons, a unit, or within exploration centers. The project was a collaboration between school-based and university-based educators. The school-based team consisted of a lead teacher liaising with the university team and individual teachers collaborating to explore CT and mathematics activities with their students. In many cases, the lead teacher was also the teacher collaborator in whose classroom the activities were implemented. The university-based collaborators, consisted of a researcher and research assistants. Although the university-based team designed and taught many of the activities, some activities were designed and taught by teachers independent of the university-based collaborators. The university-based collaborators in this case observed the implementation or showcasing of the activities, and reflected on what they observed. For the activities that the university-based team designed, the team sought and utilized practitioner input from the lead teacher as well as from the teacher collaborator before designing and before implementing the activities in the teacher collaborator’s classroom. The focus on collaborative designing of the activities reflects the university-based team’s interest in CT activities that are motivating to students but still sophisticated for teaching school curriculum and meeting a teacher’s pedagogical goals.
Figures 1 and 2. Students working on a Sphero[1] and Geometry challenge
Table 1. Contexts for CT and Mathematics in the Project
Teaching CT Concepts in Schools
Many of the classrooms listed in Table 1 had not explored computation thinking (or coding) integrated with mathematics during the school year. A few students, nonetheless, said they had explored some of the coding tools at home, in the community, in the context of another subject, or in another past class. The few classrooms which had already explored computation thinking or coding had mainly explored block programming languages, or assembling and coding robots. Thus, the activities which we designed and implemented in classrooms mainly involved introductory CT and mathematics activities, except for the Grade 5 class where we designed and implemented multiple activities over two months, hence had the opportunity to explore activities that go beyond introductory CT and mathematics activities.
Teaching practices that enable introductory CT and mathematics activities in classrooms, from our experience, appear to align with practices that enable innovative mathematics teaching and learning, which are currently promoted in several jurisdictions, including:
- teaching with hands-on materials and tools;
- teaching through problem-solving;
- integrating subjects as seen in STEM, STEAM or i-STEM efforts;
- a focus on understanding, and thinking processes and practices along with focusing on masterly of skills, facts and procedures;
- teaching through investigation, experimentation, inquiry, production and performance of knowledge, or project-based learning; and
- 21st century learning practices.
That many teachers who collaborated in the project already practiced certain innovative teaching practices was helpful as students appeared accustomed, for instance, to working with physical materials, working in groups as well as engaging in sustained learning projects.
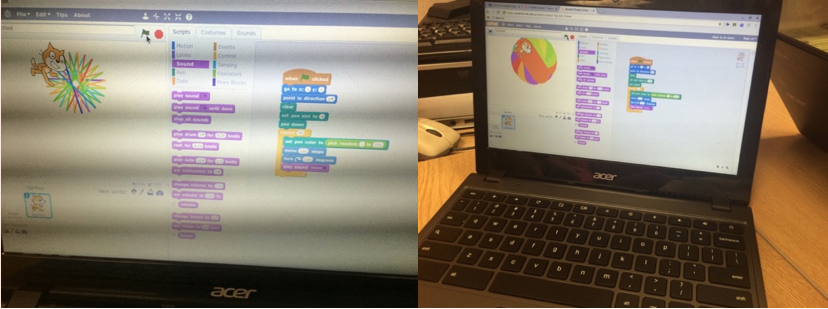
Figures 3 and 4: Scratch[2] projects for two students working in a small group
As Resnick (1998) envisions, introducing CT in schools involves both teaching a school subject through CT while teaching about CT. To integrate CT concepts and mathematics curricular concepts is to teach mathematics curricular through CT activities and at the same time teach CT concepts. This is similar to how mathematics is taught through problem solving. To teach CT and mathematics is to teach mathematics through CT tools and in the same activity teach CT through mathematics. For instance, in the CT activities we designed we addressed both CT and mathematics concepts. Gadanidis (2015) refers to this as creating a rich CT context to learning mathematics content. In a related manner, Savard and Freiman (2016) describe the “techno-pedagogical space in which technological artefacts or digital tools are considered both as tools for learning and as learning objects. Thus, programming a robot might support mathematical understanding, and mathematics can be used to understand how to code the robot” (p. 99). Teaching CT in the context of school subjects promises to offer novel learning opportunities that include creative, expressive and imaginative activities. In the past, efforts to bring these aspects in the teaching of school disciplines, through innovative teaching practices, have been constrained by activities largely limited to paper and pencil, print materials, and digital versions of these static materials.
The metaphor of CT as extending over the problem-solving process, which is also present in Wing’s (2006, 2011) definition of CT, resonates with our interest in integrating CT in school curricular. For Kalelioglu, Gülbahar and Kukul (2016) CT is about the whole process of problem solving including: identifying a problem (through abstraction, decomposition, levels thinking etc.), working with information and data needed (data practices, pattern recognition, conceptualizing etc.), planning solutions (logic, algorithms, procedures, parallelization), implementing solutions (automation, modelling, simulation) and assessing solutions (testing, debugging, generalization) for further improvement. Other metaphors such as designing computational projects, expression through a variety of computational media, computational model building are also applicable to CT.
CT is defined somewhat differently, even, by scholars such as Papert (1980), Perlis (1974), and Wing (2006) who initially advocated for the teaching of CT outside courses for computer science majors. Definitions of CT largely depend on the computer science and computation contexts that the scholar is focusing on. These context, among others, include: programming, digital design, hardware, big data and data structures, complex systems, networks, computational modelling, design and simulations. To Grover and Pea (2013) and several other scholars, earlier definitions of CT such as in NRC (2010) mainly focused on procedural thinking and on programming whereas the latter definitions such as those in NRC (2011) define CT more broadly. We find this awareness of the diversity among CT definitions and contexts helpful at understanding CT tools as well as the CT concepts, CT ways of doing as well as CT objects explored through CT tools.
Papert’s (1980) work emphasized thinking skills and “objects-to-think-with” (p. 11) that arise from working with computers. Papert argues that “learning consists of building up a set of materials and tools that one can handle and manipulate” (p. 173). Resnick and associates further develop the idea of objects-to-think-with, in the article entitled digital manipulatives: new toys to think with (Resnick, Martin, Berg, Borovoy, Colella, Kramer & Silverman, 1998). To Berland and Wilensky, the most important reason for introducing CT in K-12 curricular “is that it enables the student to use a computer” as a tool to think with (p. 630). But how best should we integrate the tool with teaching the concept (Wing, 2008)? and what are the dialects between conceptual and technical work in learning (Artigue, 2002)? In this project with Grades 4-8 we used several tools and materials in addition to computers including micro controllers and robots as tools-to-think-with in mathematics learning. As we explored which CT tools to use in the project, we asked: Which tools were appropriate for integrating introductory CT concepts with school mathematics activities in grades 4-8?
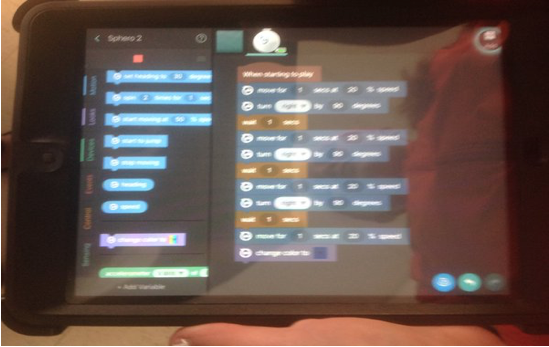
Figure 5. A screenshot of a Tickle[3] app project by a student programming the Sphero robot.
CT Tools for K-8
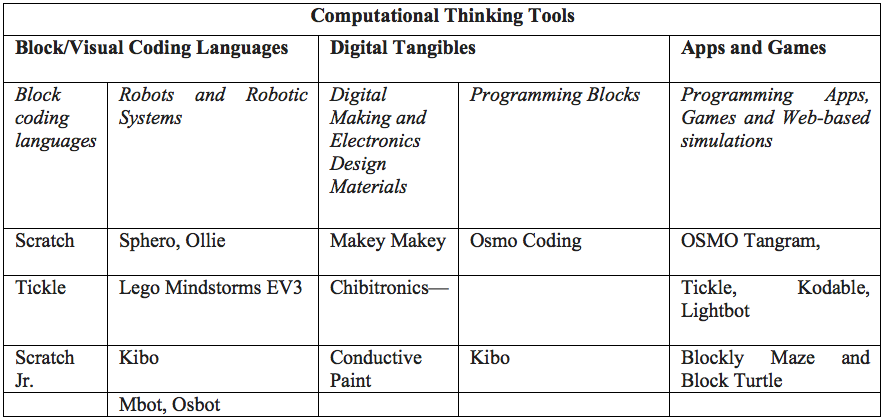
From our related work on using concrete manipulatives, virtual manipulatives and apps in teaching we have observed that tools, materials and resources selected for use in classrooms need to be grade-band appropriate, pedagogically sound, well designed as well as engaging to enable learning. As we selected the materials we continued to ask: Which of the available CT tools meet the pedagogical and curricular goals of the teachers? Brennan and Resnick (2012) comment on the “growing availability of tools that enable young people to design their own interactive media” (p. 2). Of the available tools, we narrowed our focus to CT block coding languages, robots, digital making materials, programming blocks, as well as programming apps and games. We also reflected on how the CT tools available related to each other. Table 2 shows the specific tools we have used so far. The tools are grouped under three broader categories into which we see the tools to fit: Block/Visual Coding Languages, Digital Tangibles, Apps and Games.
Table 2. CT Tools used in our work with Grades 4-8 students
Brennan and Resnick (2012) outline not only CT concepts but also CT practices and CT perspectives observed among children and youth who created projects using a visual block-based coding language, Scratch (See figures 3 and 4). CT concepts in the context of Scratch, per Brennan and Resnick, include sequences, loops, parallelism, events, conditionals, operators, and data. CT practices include: being incremental and iterative, testing and debugging, reusing and remixing, and abstracting and modularizing. And the perspectives which Brennan and Resnick identified among Scratch users included: expressing, connecting, and questioning.
Robots and robotic systems are currently used as educational tools but mostly in extra-curricular and outside school contexts (Savard & Freiman, 2016). There are calls for the integration of robots in classrooms to expand the reported benefits of working with robots for children and youth. Programming apps and designing games are another context used to learn and practice CT concepts. In a similar manner to mathematics learning apps that are designed to teach mathematics concepts, programming apps are designed to teach programming concepts.
Digital tangibles are defined by Price and Pontual Falcão (2011) as “physical artefacts designed to trigger various digital events, potentially provide innovative ways for children to play and learn” (p. 500). Resnick et al. (1998) uses the term digital manipulatives and define digital manipulatives as manipulatives embedded “with communication power.” Resnick (1996) observed: “digital manipulatives embed computational capabilities inside traditional children’s toys—such as blocks.” (p. 44). Digital manipulatives are “computationally enhanced” (Zuckerman, Arida & Resnick, 2005, p. 859). Other researchers have referred to these materials as augmented reality teaching tools (Mateu, Lasala, & Alamán, 2014; Price & Pontual Falcão, 2011) or intelligent manipulatives (Geurts, Vanden Abeele, Van Keer, & Isenborghs 2014).
Programming blocks are usually assembled in kits for building programs or for assembling robots. Children manipulate different wooden blocks to write their own programs (Wang, Zhang & Chen, 2013) or to assemble and then program robots. The kits include several blocks, each with specific semantics such as motion commands, start and end blocks, direction blocks, logic, actuator, utility and sensor blocks, as well as variables. Programming blocks involve physical actions and interactions.
CT User Interfaces
We found the framework that focuses on the interfaces of the CT tools and how the interfaces influence user’s actions and interactions helpful when selecting CT tools to use and when considering classroom practices supporting the use of these tools. Most CT tools appear to have emerged from the quest to make computer science and computational contexts more learner friendly than the symbolic, syntax-based programming languages. The framework on user interfaces arises from four distinct fields, which inform the design and study of CT tools and materials:
- The human-computer interaction field, HCI, in which interfaces are identified by the interactions they afford to the users: For example, interfaces are categorized into: graphical interfaces, tangible interfaces, multi-touch interfaces, multi-user or shared interfaces. More recently innovated interfaces such as touch-tables (which can be touched by several users) are compared to user interfaces which use a keyboard and mouse. Interfaces that use a screen, mouse and keyboard are referred to as graphical user interfaces, or point and click interfaces. On the other hand, tangible interfaces involve materials that can be physically manipulated. These materials are also referred to as graspable interfaces. The term hybrid user interface describes interfaces that involve both graphical and tangible interfaces. Touch tables are examples of multi-touch and multi-user interfaces because they can be interactively touched anywhere on the screen and by several users. Smart phone, tablet devices and other devices with touch screens fit the category of multi-touch interfaces.
- The field of designing digital technologies for teaching children, youth and novices programming skills championed by Papert and associates: Tools for teaching CT concepts including programming and complexity thinking concepts are designed and investigated in this field. The tools include friendly programing tools for children and youth. Block coding languages, for instance, accessed on computers and tablets, following HCI language, are referred to as graphical programming languages (Brennan & Resnick, 2012), whereas digital materials which may be accessed without computers are referred to as tangible programming tools or digital manipulatives (Resnick et el., 1998). Programming blocks and programming robots have been designed for much younger children based on the conceptual and empirical reasons that tangible programming materials are more inviting and enjoyable (Horn, Crouser and & Bers, 2012). Young children produce fewer errors with tangible programming materials, need less time to accomplish the tasks when using tangible programming materials than when using graphical programming environments (Sapounidis, Demetriadis & Stamelos, 2015).
- The field of computer science education at college and university where computer science is taught under separate courses to students interested in computer science: Here the teaching of programming to novice programmers and to students not majoring in computer science is explored. More friendly programming languages, usually visual programming languages, are explored.
- And, to a certain extent, the field of curriculum education research focusing on teaching computer science, originally, in high schools but more recently including K-8 schools. This field is beginning to fuel the development of new tools (Grover & Pea, 2013) which are put in use, and their utility, pedagogy, constraints and benefits are investigated
Figure 6. A student creates a card with Chibitronics[4] materials
We have outlined the fields in which CT tools are designed and investigated because these fields offer a classification of available CT tools by interface, actions and interactions as: Textual (also referred to as symbolic), graphical (also, visual), tangible (graspable), multi-touch (touch screen), multi-user (touch surfaces), or hybrid tools (graphical and tangible). In the HCI field, these terms apply to user interfaces whereas in the design of digital learning technologies field several terms apply including tools, languages, representations, physical materials or environments. This focus on user interfaces introduces several acronyms: GUI for graphical user interfaces, TUI for tangible user interfaces (e.g., Ras, Krkovic, Greiff & Isenborghs, 2014), MUI for multi-touch and multi-user interfaces (Mateu et al., 2014; Schneider et al., 2011). Strawhacker and Bers (2015) observe that these terms are used somewhat differently in HCI than in digital learning technologies research. In HCI, for example, MUI takes on more technical meanings than multi-touch: MUI in HCI is used to refer to multi-user, space multi-plexed, co-located interfaces because these tools are designed to be manipulated by more than one person and the tools open possibilities for reflection and collaboration among several users concurrently manipulating the same device. Mateu et al. talk about Natural User Interfaces, NUI that are based on “gestural interactions” and compares them to tangible user interfaces that are “based on interaction with physical objects’ (p. 815). The classification GUI, TUI, MUI and HUI is applicable to the CT tools in Table 2.
Figure 7. Students exploring assembling and programming robots to move in specified paths`
Figure 8. Students using the Makey Makey[5] kit listen to patterns played on a piano app as well as to talk about conductivity.
Planning Activities for Varied CT User Interfaces.
GUI: We found that the graphical programming languages such as Scratch (Figures 3 and 4) and other internet or device-based CT programming apps and games, we selected to use, mainly fell under the category of graphical user interfaces, GUI. In terms of materials needed for activities in which these tools were used, only the computer, keyboard and mouse were required. We observed that with these tools learners could work at their desks using chrome or netbooks, or could use computers in the classroom or lab, and that learners were also comfortable working individually or in pairs. These materials were also easily accessible by students in the classroom and at home for continued CT activities.
TUI: For the digital making materials, such as Chibitronics (Figure 6) and Bare Conductive electric paint[6], for which learners did not need a device with a screen, as well as for robots such as Kibo and Cubetto[7] that did not need to be programmed on a computer or touch-screen device,[8] these tools fall under the category of tangible user interfaces, TUI. Learners needed large desk space to work with TUIs. In some cases, they also worked on the floor or in the hallway. Learners could comfortably work in small groups of 3 to 5 students when using these materials. Some of these materials such as conductive tape and LED lights are available in bulk at general hardware or electronic stores.
MUI: Tools such as programming apps and programming games, that required only a touch-screen mobile device fit under the category multi-touch user interfaces, multi-touch MUI. We observed learners comfortably working individually or in pairs with tablet devices in classrooms. When students elected to use their own pocket devices such as i-pods, the pocket devices were more conducive to working individually than in pairs or small groups. For repeated use these tools could also be accessed in classroom and at home where learners have access to touch screen devices.
Tools that could be manipulated by various users on a tabletop or on the floor fit under the category of multi-user MUI. Digital making materials and standalone robots that students did not have to program on a computer, or could download a program onto the robot as is the case with m-Bot[9] (Figure 7) fit under the category of multi-user MUIs in addition to being TUIs. Learners comfortably worked in groups of three to five learners during activities on MUI tools. Learners needed access to these tools and materials to be able to continue to use them at school or at home.
HUI: Tools for which both tangible materials such as programming blocks and robots as well as screen-based devices (e.g., tablet or computer devices) are incorporated fit under the hybrid user interfaces, HUI. Most robots and blocks that are programmed on screen-based devices fit under this category. Examples of hybrid tools are the Makey Makey microcontroller kit (Figure 8) with which students work with materials as well as a device that has a USB port — such as on a computer, Netbook or Chromebook. Robots such as Sphero (Figures 1 & 2) which are programmed on a touch-screen device using an app, are examples of HUIs. Another example of HUIs is the Osmo coding kit[10] for which blocks laid on a flat surface, with the aid of Osmo accessories — the mirror and the base — program an app on an iOS tablet. A few of the learners mentioned that they had previously interacted with robots and digital blocks at home. Continued use of these tools is limited by availability of these digital materials at school or at home.
We observed that students worked comfortably in small groups when working with tools that could be laid on tabletops or tools that could be placed on the floor such as several of the robots, as compared to activities that only required a computer, net- or chrome-book.
Tools such as board games that teach both programing and mathematics using physical boards that are not digitally embedded were simply physical materials for teaching programming and other CT concepts. In the project, we also explored a category of tools that bore resemblances to programming tools. Osmo tangrams share the base and mirror materials with Osmo coding. Tiggly[11] counting, Tiggly addition and Tiggly number line utilize digitally embedded physical tools with silicone touch points that when tapped on a tablet device, the tablet reacts to them just like it does to a fingertip touch. These tools fit the category of digital tangibles and MUI for learning mathematics concepts. Both Osmo and Tiggly are in the company of tools for teaching other school disciplines such as languages and the arts. We found these tools useful to explore among CT tools because, in the project they helped learners in early grades, where needed, to get used to working in more than one interfaces, hybrid interfaces. As well, tools with hybrid interfaces prompted learners to talk about digital hardware and user interfaces, which are aspects of CT.
Figure 9. Students observe a Lego Mindstorms EV3[12] they assembled and programmed
Parallels between Mathematics and CT tools
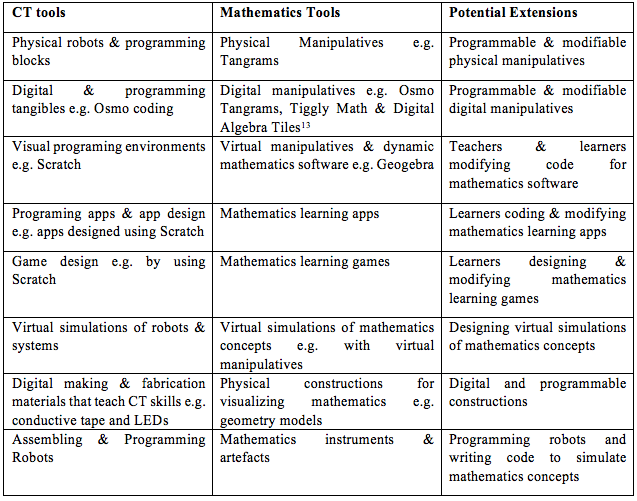
The use of materials for teaching and learning in schools is a critical issue for many reasons but particularly because several commercial materials are increasingly available in classrooms and their access is receiving wide institutional and community support. Tools developed for CT have parallels in mathematics education. Several scholars in both the digital learning technologies and HCI field turn to early childhood learning as well to mathematics education while they seek to understand the potential role of tangible programming tools (e.g., Manches & O’Malley, 2012). As we reflected on our use of CT tools in teaching grades 4-8 CT and mathematics we drew some potential parallels between CT learning tools and mathematics learning tools. These parallels are shown in Table 3. Parallels that potentially exist between CT and mathematics tools aside, CT tools appear to promise to extend the affordances of mathematics tools as shown in the third row of Table 3.
Table 3. Parallels between CT and Mathematics Tools
Akin to the innovation of virtual manipulatives and mathematics learning apps that complemented earlier physical tools (Namukasa, Stanley & Tutchie, 2009; Namukasa, Gadanidis, Sarina, Scucuglia & Aryee, 2016), in our view, CT tools complement earlier physical tools and are not as limited to simulating less sophisticated concepts. They have the potential to represent and simulate abstract, advanced and complex concepts. More abstract concepts could be learned with the help of, for instance, block programming languages, robots as well as app development. CT tools promise to add the following materials, interfaces, abilities and objects to the teaching and learning of mathematics:
- Digitally embedded physical materials that are counterparts to physical materials
- Hybrid tools that combine symbolic, graphical, and tangible interfaces
- Affordances to create (design, code, simulate, make, fabricate) as well as modify learning objects.
- CT learning objects designed by students and teachers including, but not limited to, code, projects, games, apps, robot commands, and robots.
Concluding Remarks
CT and curricular learning activities need to be carefully planned to ensure that CT tools are approached from a pedagogical perspective. In this article, we have shared some of the tools we have used to integrate introductory CT concepts and mathematics curricular concepts. We have shared a categorization of these tools by interfaces, thus showing differences and similarities among the tools based on interactions afforded to users. We have also mentioned implications of interfaces on the accessibility of CT tools in school and at home. It is worth noting that challenges exist when adopting CT tools for teaching mathematics. Gadanidis (2015) notes the challenge of designing learning experiences that afford students to engage is sophisticated mathematics and CT concepts. Because some of the tools such as Scratch could be used to teach several other concepts and curricular subjects, activities need to be carefully planned for the targeted learning. Some CT tools appear to have limited potential when integrating CT concepts with mathematics curricular topics. We are further considering activity design and the pedagogy of integrating CT and mathematics. Another implication of this exploration of CT tools and materials is that some activities with selected CT tools fit the category of unplugged activities.
Classifying CT tools by interfaces adds another kind of unplugged[1] activities that are observed to be a major component of the pedagogical model for K-12 CT activities identified by Kotsopoulos, Floyd, Khan, Namukasa, Somanath, Weber, & Yiu (2017). We see, digital tangibles and digital making materials such as programming blocks and digital crafts, TUIs that do not involve a screen-based device, to fit under unplugged activities. Thus, when we need to include unplugged activities, such as in a double lesson, we have included TUI activities. Further, this classification of tools by user interface is helpful when planning CT activities for extended lessons.
For extended curricular lessons such as blocks of lessons or consecutive lessons in a week of CT and mathematics activities, two possibilities worked well for us: learning in-depth through one tool such as Scratch or Sphero, or designing exploration centers in which more than one tool was available for learners to explore. With the exploration centers, we varied tools among GUIs, TUIs, MUIs and HUIs tools but still focused on related mathematics concepts such as on motion and transformation geometry as well as measurement. Exploration centers worked well when the goal was introductory CT concepts and mathematics as compared to, what we have come to refer to as, intermediate or, even, advanced CT skills.
The major difference we found when utilizing CT tools in extended curricular lessons was that tools such as Scratch and Sphero were more versatile in a way that they could be used to integrate several CT and mathematics concepts and could be taught in several lessons such as: Scratch I and Geometry, Scratch II and Geometry, and Scratch III and Geometry; or, Scratch and Geometry, Scratch and Measurement, and Scratch and Patterning; or, Introduction to Sphero and Mathematics, Intermediate Sphero and Mathematics, and Advanced Sphero and Mathematics. Yet for other tools, such as programming blocks, especially those designed for much younger children, a single school block of about two hours was adequate to explore CT and mathematics through the tool. We do not know if the versatility of the Sphero — an app-enabled — robot and the Scratch — a block-programming language — for example, is because these tools are screen-based (i.e., are GUIs in the case of Scratch and enabled on a MUI in the case of Sphero) as contrasted to TUI tools that do not involve screen-based devices.
In the Grade 5 sub-urban classroom we designed a set of 7 exploration centers, including Scratch and Sphero activities, of CT and mathematics activities. Each center was stationed at one group of tables and took up to 30 minutes to complete before the group of students who worked together rotated to the next center. (For classrooms which were not familiar with coding, we begun with a 20-minute presentation about what coding is and where it is used in life before breaking out in exploration centers.) As students worked at different centers, the classroom teacher, one member of the university-based team, and one volunteer circulated in the classroom to help respond to students’ questions, and to observe as well as document students’ projects. (In some other classrooms we were privileged to have an additional volunteer or observer.) At the end of every lesson block, before a regular school break, a few minutes were devoted to debriefing about the activities. Due to limitation of space we only share the list of the exploration centers explored in the Grade 5 sub-urban classroom:
- Sphero II (a TUI programmed on a MUI)
- OSMO Coding Challenge (a HUI with both TUI and MUI)
- Blockly[2] Maze and Turtle Challenge (could be played on a GUI-computer or MUI- touch screen)
- Chibitronics Greeting Card design (a TUI)
- Patterns and Makey Makey (a TUI connected to a GUI)
- M-Bot and other bots (TUIs)
- Scratch II Challenge (a GUI)
- Kibo and Cubetto coding blocks and robots (a TUI)
During the exploration centers, students explored the following CT concepts — motion commands, parameters, loops/repetition, sequences, algorithm building, user interface events and reusing; as well as the following mathematics curricular concepts — motion and turns/angles geometry, length, distances and time measurements, and proportions. Fewer exploration centers were completed where only a block of lessons as opposed much of the day was available for CT and mathematics activities.
Highfield and Savard (2016), similarly, utilized exploration centers which involved different activities but with only the two similar tools, pro-bot and bee-bot robots. We agree with Brennan and Resnick (2012) and Grover and Pea (2013) that there is a growing number tools for teaching CT concepts. “Most children today are facile with the mechanics of using the tool and are not afraid to explore and play with it” (Wing, 2008 p. 3721). Learners are not only tool users but also the “growing availability of tools … enable young people to design their own” tools (Brennan & Resnick, 2012, p. 2). Learners, given their interest in electronic tools and in digital and non-digital making, are excited to learn to use CT tools. This presents an opportunity to design activities for learning both the tool and curricular concepts – CT and mathematics, in this case— taught through using the tool.
Acknowledgements:
The outreach project reported in this paper is part of a research project funded by the Social Sciences and Humanities Research Council of Canada.
References.
Artigue, M. (2002). Learning mathematics in a CAS environment: The genesis of a reflection about instrumentation and the dialectics between technical and conceptual work. International Journal of Computers for Mathematical Learning, 7(3), 245-274.
Berland, M., & Wilensky, U. (2015). Comparing virtual and physical robotics environments for supporting complex systems and computational thinking. Journal of Science Education and Technology, 24(5), 628-647.
Brennan, K., & Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking. A paper presented at AERA, 2012. Available at web.media.mit.edu/~kbrennan/files/Brennan_Resnick_AERA2012_CT.pdf.
Kotsopoulos, D., Floyd, L., Khan, S., Namukasa, I. K., Somanath, S., Weber, J., & Yiu, C. (In press). A Pedagogical Framework for Computational Thinking. Digital Experiences in Mathematics Education.
Gadanidis (2015). Coding as a trojan horse for mathematics education reform. The Journal of Computers in Mathematics and Science Teaching, 34(2), 155-173.
Geurts, L., Vanden Abeele, V., Van Keer, K., & Isenborghs, R. (2014). Playfully learning visual perspective taking skills with Sifteo cubes. Proceedings of the First ACM SIGCHI Annual Symposium on Computer-Human Interaction in Play, pp. 107-113.
Grover, S. & Pea, R. (2013). Computational thinking in K-12: A review of the state of the field. Educational Researcher, 42(1), 38-43.
Highfield, K., & Savard, A. (2016). Robotic Tasks: Affordances for mathematics Learning? 13th International Congress on Mathematics education, ICME-13. Hamburg, Germany.
Horn, M. S., Crouser, R. J., & Bers, M. U. (2012). Tangible interaction and learning: The case for a hybrid approach. Personal and Ubiquitous Computing, 16(4), 379-389.
Kalelioglu, F., Gülbahar, Y., & Kukul, V. (2016). A framework for computational thinking based on a systematic research review. Baltic Journal of Modern Computing, 4(3), 583.
Manches, A., & O’Malley, C. (2012). Tangibles for learning: A representational analysis of physical manipulation. Personal and Ubiquitous Computing, 16(4), 405-419.
Mateu, J., Lasala, M. J., & Alamán, X. (2014). Virtual Touch: A tool for developing mixed reality educational applications and an example of use for inclusive education. International Journal of Human – Computer Interaction, 30(10), 815-828.
Namukasa I, K., Gadanidis, G., Sarina, V., Scucuglia, R., & Aryee K. (2016). Selection of apps for teaching difficult mathematics topics: concrete props, virtual applets and touch pad apps. In P. Moyer-Packenham (Eds.), International Perspectives on Teaching and Learning Mathematics with Virtual Manipulatives (pp. 275-300). Dordrecht: Springer.
Namukasa, I. K., Stanley, D., & Tutchie, M. (2009). Virtual Manipulative Materials in Secondary Mathematics: A Theoretical Discussion. Journal of Computers in Mathematics and Science Teaching, 28(3), 277–307.
National Research Council, NRC. (2010). Committee for the Workshops on Computational Thinking: Report of a workshop on the scope and nature of computational thinking. Washington, DC: National Academies Press.
National Research Council, NRC. (2011). Committee for the Workshops on Computational Thinking: Report of a workshop of pedagogical aspects of computational thinking. Washington, DC: National Academies Press.
Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. New York: Basic Books.
Perlis A. J. (1974). The computer in the university. In M. Greenberger (Ed.), Computers and the world of the future (pp. 180-199). Cambridge, Mass: M.I.T.
Price, S., & Pontual Falcão, T. (2011). Where the attention is: Discovery learning in novel tangible environments. Interacting with Computers, 23(5), 499-512.
Ras, E., Krkovic, K., Greiff, S., Tobias, E., & Maquil, V. (2014). Moving towards the assessment of collaborative problem solving skills with a tangible user interface. TOJET: The Turkish Online Journal of Educational Technology, 13(4), 95-104.
Resnick, M. (1998). Technologies for lifelong kindergarten. Educational Technology Research and Development, 46(4), 43-55.
Resnick, M., Martin, F., Berg, R., Borovoy, R., Colella, V., Kramer, K., & Silverman, B. (1998). Digital manipulatives: New toys to think with. Proceedings of the SIGCHI Conference on human factors in computing systems, 281-287. ACM Press/Addison-Wesley.
Rick, J. (2010). Quadratic: Manipulating algebraic expressions on an interactive tabletop. Proceedings of the 9th International Conference on interaction design and children, ACM, 304-307.
Sapounidis, T., Demetriadis, S., & Stamelos, I. (2015). Evaluating children performance with graphical and tangible robot programming tools. Personal and Ubiquitous Computing, 19(1), 225-237.
Schneider, B., Jermann, P., Zufferey, G., & Dillenbourg, P. (2011). Benefits of a tangible interface for collaborative learning and interaction. IEEE Transactions on Learning Technologies, 4(3), 222-232.
Smith, S. (2013). Through the teacher’s eyes: Unpacking the TPACK of digital fabrication integration in middle school language arts. Journal of Research on Technology in Education, 46(2), 207.
Strawhacker, A., & Bers, M. U. (2015). “I want my robot to look for food”: Comparing Kindergartner’s programming comprehension using tangible, graphic, and hybrid user interfaces. International Journal of Technology and Design Education, 25(3), 293-319.
Savard, A., & Freiman, V. (2016). Investigating complexity to assess student learning from a robotics-based task. Digital Experiences in Mathematics Education, 2(2), 93-114.
Wang, D., Zhang, Y., & Chen, S. (2013). E-block: A tangible programming tool with graphical blocks. Mathematical Problems in Engineering, 1-10.
Wing, J. M. (2008). Computational thinking and thinking about computing. Philosophical Transactions of the Royal Society, 366, 3717–3725.
Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33-35.
Zuckerman, O., Arida, S., & Resnick, M. (2005). Extending tangible interfaces for education: Digital Montessori-inspired manipulatives. CHI 2005: Technology, Safety, Community: Conference Proceedings – Conference on Human Factors in Computing Systems, pp. 859-868.
Notes.
[1] The Sphero and SPRK+ (the transparent version of Sphero) Robots are designed by Sphero, formerly Orbotix. They are available at http://www.sphero.com/. Sphero produces other robots such as BB-8 and Ollie that are similarly app-enabled robots.
[2] Scratch, a visual block-based programming languages for younger programmers was developed by The MIT Media Lab’s Lifelong Kindergarten group, led by Mitchel Resnick, and is available at https://scratch.mit.edu/.
[3] The Tickle app, a block-based programming app, is available at both iTunes and Google play store: https://tickleapp.com/. It is developed by the Tickle Labs Inc.
[4] Chibitronics, a kit for circuitry craft materials including conductive tape, LED, lights sensors, effectors and a microcontroller, is developed by Chibitronics PTE ltd and information on it is available at https://chibitronics.com/.
[5] http://makeymakey.com/apps/. Makey Makey is a micro controller developed by JoyLabz LLC.
[6] Bare conductive paint, a coding craft material, is a product of Bare Conductive with information available at https://www.bareconductive.com/.
[7] Cubetto, a robot for younger kids programmed on programming blocks and a programming board, is a product of Primo Toys and is available at https://www.primotoys.com/.
[8] Available at http://kinderlabrobotics.com/kibo/, Kibo —a product of Kinder Lab Robotics — is a robot programmed by scanning programming blocks.
[9] Available at www.makeblock.com/mbot-v1-1-stem-educational-robot-kit, mBot is designed by Makeblock Co.
[10] Available at https://www.playosmo.com, Osmo coding is a product of Tangible Play.
[11] Available at https://www.tiggly.com/, Tiggly Math (counting, addition, and number line) are a product of Tiggly
[12] Available at http://www.lego.com/en-us/mindstorms, Lego Mindstorms EV3 is developed by the LEGO group which develops several other series of Lego robot kits.
[13] Rick (2010) investigates digital algebra tiles on a touch table.
[14] For several other unplugged activities see http://csunplugged.org/
[15] Available at https://blockly-games.appspot.com/ Blockly Maze and Blocky Turtle game are designed by Blockly Games Beta which has designed several other games for teaching programming.