By Betty Zhang & Iain Brodie
Coding allows us to add further dimensions to our learning of mathematics, and it is time that we reclaim it from the computer science field in order to address the needs of our 21st century learners. Incorporating computational thinking into our learning allows us to add wide walls to our low floor, high ceiling mathematics activities. In other words, besides designing learning engagements that are easy to start and get progressively more complex, we need to allow for different approaches and learning styles. Coding and computational thinking allow us to have students practice being resilient through dealing with complex problems that need time to solve.
Resilience is a popular topic these days, and while it is something that we can lead students to appreciate and develop, we need to provide safe opportunities for them to be resilient. Such opportunity landed on our doorstep when we were asked if we would like to beta test a new online coding app, Number Patterns and Sets, developed by George Gadanidis at https://researchideas.ca/numbers/. The big idea behind the app was to get students to play with and understand Boolean algebra logic ideas like AND, OR and NOT. This was wrapped up in a simple landscape of a 100s chart onto which you could splash colours, colour in the squares or have a cute, animated Gork smile at you from the squares you chose. All you had to do to create patterns was play with the coding blocks from Blockly to see what you would get.
The online codin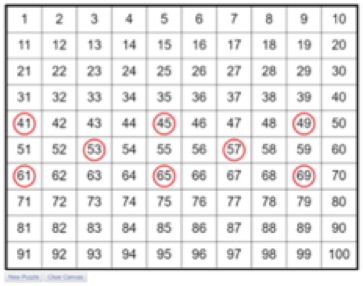 g app can randomly generate puzzles for students to practice pattern recognition, sharpen their number sense, and use a simple programming language to problem solve. The app circles certain numbers with an observable pattern and the students need to code an algorithm that will block out these specific numbers.
g app can randomly generate puzzles for students to practice pattern recognition, sharpen their number sense, and use a simple programming language to problem solve. The app circles certain numbers with an observable pattern and the students need to code an algorithm that will block out these specific numbers.
Pretty soon, some students started to solve one puzzle after another without giving it much thought because they had discovered a clever trick. By simply changing a few inputs of the provided code, they could solve every puzzle in a few seconds. It was amazing how quickly they had noticed this, but it also pointed out the need to increase the c omplexity level of the puzzles to challenge the students’ mathematical thinking further. Instead of adhering to a regular number pattern per puzzle, we thought about how we might combine different patterns and codes to paint a picture.
omplexity level of the puzzles to challenge the students’ mathematical thinking further. Instead of adhering to a regular number pattern per puzzle, we thought about how we might combine different patterns and codes to paint a picture.
Being someone who has never coded before, I had the opportunity to experience firsthand the frustration and discovery that students may find when they create their first code. It was an addicting experience. I happily discovered that I could change the dimensions of the chart to 12 by 12 because I wanted a large canvas to paint with code. Initially, I only wanted to create a simple landscape with water, mountains, and flowers to familiarize myself with the language of coding. Soon after I discovered how rewarding it was to watch the app paint what I had created through programming, I could not help but to add more details and then hit “Run Code” to see the newly added renditions. I could have painted it layer by layer but I wanted to find more elegant solutions that used Boolean logic and more complicated number theory. After multiple attempts and a very long code, I made my first painting through coding. I encouraged the students to paint something as well because I also wanted them to experience the joy, challenge, excitement, and pride in creating something beautifully complex with their mathematical minds.
At the base level of painting pictures on a number grid, the students could write code to individually ‘paint’ each block. The beautiful thing about starting this way is that it is 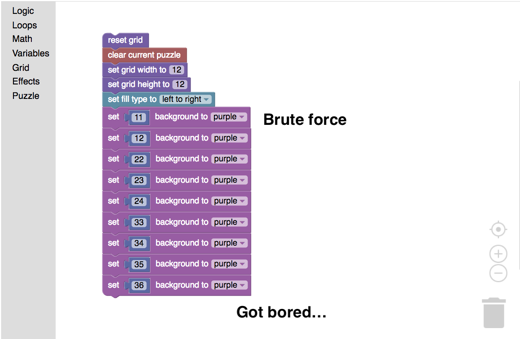 repetitive and somewhat tedious to do. After using this ‘brute force’ method, students pretty soon start looking for shortcuts in order to make their work easier. This leads them into using higher order thinking skills, and begins to develop an aesthetic sensibility for efficient or clever code. In the end, not only do they create an aesthetically pleasing picture, but they do it through an efficient combination of complex mathematical concepts and coding.
repetitive and somewhat tedious to do. After using this ‘brute force’ method, students pretty soon start looking for shortcuts in order to make their work easier. This leads them into using higher order thinking skills, and begins to develop an aesthetic sensibility for efficient or clever code. In the end, not only do they create an aesthetically pleasing picture, but they do it through an efficient combination of complex mathematical concepts and coding.
An important part of writing code to complete a task is that the task can be accomplished through persistence and resilience. It might take hard work, it might require us to think in ways that we do not normally in mathematics class, but it can be done. What is interesting about approaching the learning of Boolean terms through coding a picture is the rich landscape the students dove into in order to find patterns that would paint their pictures. Imagine trying to write a nice neat c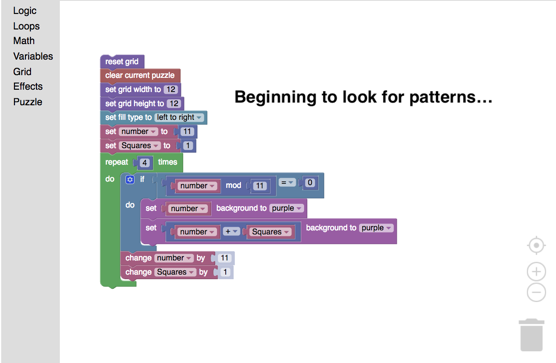 ode for the light purple cloud at the top right of the picture. You might notice that each line begins with a multiple of 11, then that each successive line has one more member than the previous one. Maybe we could start with the instruction to colour in multiples of 11 OR multiples of 12? Greater than 10? Less than 49? Remainder when divided by 11 is more than 4? What numbers does this miss? How can we describe all of this in Blockly so that the computer paints the cloud we want? Instead of creating code to fit a pattern, the students were problem-solving to find patterns in blocks of numbers that they could address in as brief a set of code blocks as possible. The surprising byproducts of this activity are not just great mathematical learning, but resilience, higher order thinking and a sense of aesthetics.
ode for the light purple cloud at the top right of the picture. You might notice that each line begins with a multiple of 11, then that each successive line has one more member than the previous one. Maybe we could start with the instruction to colour in multiples of 11 OR multiples of 12? Greater than 10? Less than 49? Remainder when divided by 11 is more than 4? What numbers does this miss? How can we describe all of this in Blockly so that the computer paints the cloud we want? Instead of creating code to fit a pattern, the students were problem-solving to find patterns in blocks of numbers that they could address in as brief a set of code blocks as possible. The surprising byproducts of this activity are not just great mathematical learning, but resilience, higher order thinking and a sense of aesthetics.
With coding at the intersection of math and art, we were able to learn much more than we had set out to do. If we had just learned how to use some Boolean terms to make our code more efficient, we would have marked the lesson a success, but in adding an arts layer over top of the number puzzles we learned much more. Instead of looking for rules to follow a pattern, we were looking for patterns where not just one might exist. This let us 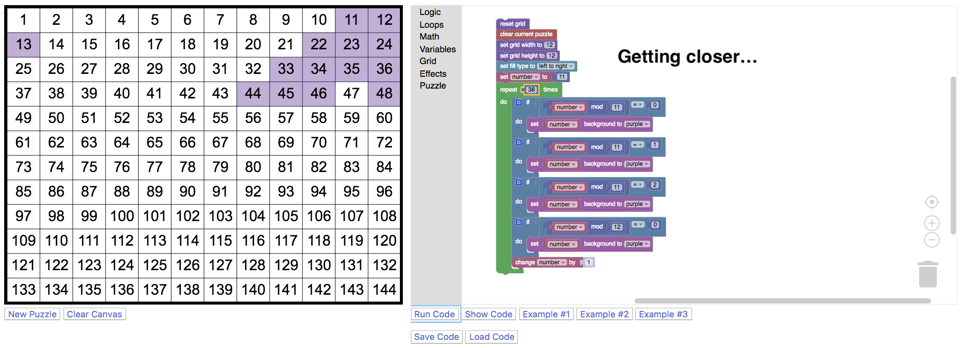 really use the Boolean terms to include, exclude, and combine different bits of code that would allow us to paint a region of the number chart. Here we had wide walls that let us learn from different directions, but also broadened our learning horizons to include complex mathematics, interesting visual arts, as well as the aesthetics of efficient code. We now have a new level for what we consider a successful lesson.
really use the Boolean terms to include, exclude, and combine different bits of code that would allow us to paint a region of the number chart. Here we had wide walls that let us learn from different directions, but also broadened our learning horizons to include complex mathematics, interesting visual arts, as well as the aesthetics of efficient code. We now have a new level for what we consider a successful lesson.
Betty Zhang is a new teacher with two years’ experience teaching in the UK near London. Now back in Canada, she is pursuing a Masters of Professional Education (MPED) degree in mathematics curriculum.
Iain Brodie is an elementary teacher with twenty-eight years’ experience teaching from grade one to grade eight in Scarborough, Ontario.
