Namukasa I. K.
Too often educators seek to identify computer programming tasks that also meet specific curricular goals. Such tasks may engage students in reviewing old or in learning new content and processes. In this paper, I share a task that applied computational programming in mathematics lessons, the path and polygon construction activities. This task, in a manner similar to certain CT activities, enabled the consolidation of learning. To be specific, I elaborate on the computational thinking (CT), the mathematics, as well as the CT and Mathematics integrated concepts enabled by the task.
Path and Polygon Construction CT Activities: In the middle grades classrooms, where these activities were taught, students planned and programmed robots or screen characters to navigate defined paths, usually shapes. For example, students coded a robot to navigate around the room, in the hall way, on a play field, or along a polygon path marked with tape on the floor. They also coded a screen character to move from a starting point to an end, while making specific turns, covering distances, moving at specific speeds, outlining perimeters, enclosing an area, avoiding obstacles, or tracing a shape.
Figure 1. Geometry and path constructions
[Original code for Scratch Construction by Betty Zhang; https://scratch.mit.edu/projects/197671573/]
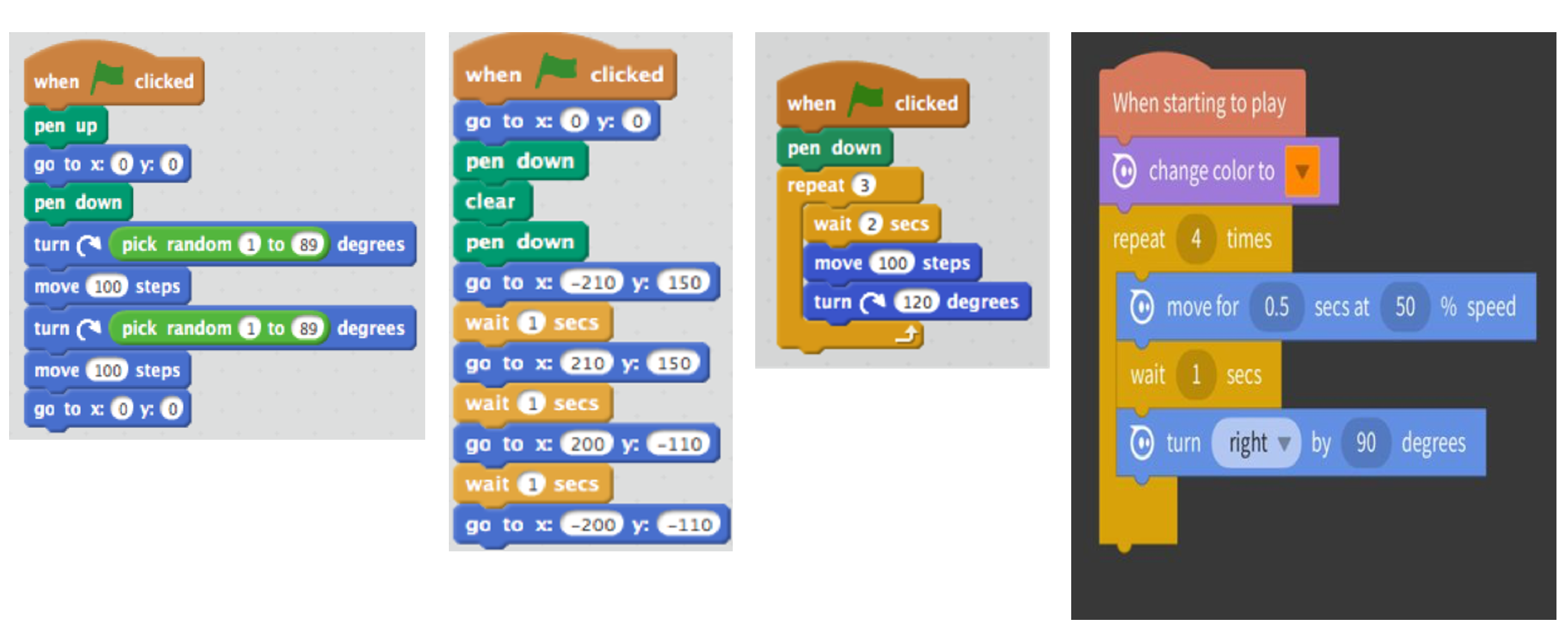
As shown in the sample codes in Figure 2, the assembling of commands to move and turn robots, utilizes task commands that involve movement and direction, logic blocks such as iterations (repeat) and conditional logic (e.g., if-then loops) for patterned movements as well as filling in the in the blanks for the magnitudes (i.e., parameters) on the blocks to specify, say, attributes such as lengths, time lapses and speeds of the movements. Students also explored several other blocks such as the functions blocks. When assembling commands for moving characters on screen using Scratch, they made new blocks (i.e., by combining several commands in one new command). Students also assembled control and event blocks (e.g., when to start, how long to pause between movements, or sensing an obstacle) as well as utilized drawing blocks (such as pen up/down blocks).
As students wrote or modified code for drawing and tracing, they had opportunities to study the geometrical properties of polygons, shapes, lines, turns and curves, displacement and motion, as well as relations among these properties. They were also able, when prompted, to write code that randomly generated polygons, such as the code in Figure 2 for creating acute triangles of different sizes. Students picked random parameters. They explored the geometry concepts, and thus reinforced their understanding of the curricular concepts of geometrical properties and relationships as well as their grasp of measurement attributes.
Figure 2. Varied codes for paths and geometrical figures
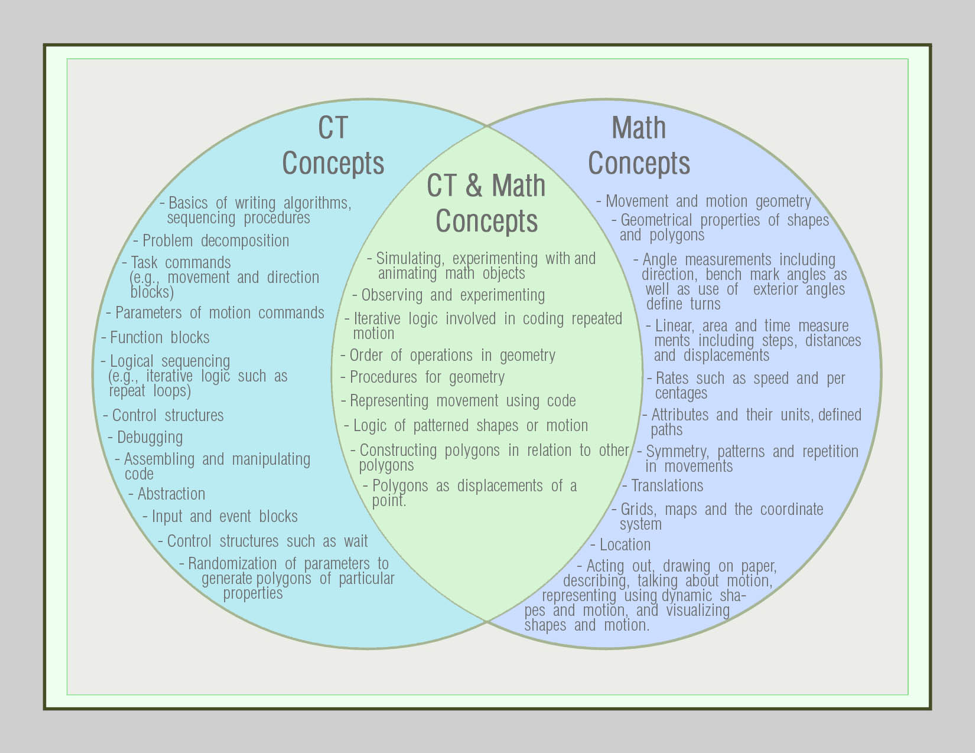
Students also explored concepts that appeared to be at the confluence of CT and mathematics. For example, the path and polygon construction activities appeared to provide opportunities for them to simulate and visualize motion in the physical space of robots or the visual space of screen characters. This also applied when students animated screen characters. Because the simulations and animations were also represented by steps of code in the semi-symbolic spaces of blocks of code, this made it possible for them to link code representations with the representations in the physical and visual areas. Table 5 summarizes the concepts that students appeared to encounter in the path and polygon drawing or tracing activities.
Figure 3. Concepts and processes encountered in Path and Polygon Construction CT Activities
The task elaborated on in this paper evinces that when students are engaged in CT activities that are designed with Curricular in mind such as the paths and polygon construction activities, they get the opportunity to review concepts, to learn concepts related to curriculum content, to explore some concepts that they would have normally explored at latter grades. They are also exposed to encounter more abstract and new treatment of concepts. The integration of computational thinking and curricular is helpful at exploring new, different and advanced concepts in addition to providing a novel context for reviewing curricular content covered at or in earlier grades.
More CT activities and their corresponding pedagogies are explored in articles featured in this issue of the Math and Code ‘Zine: In the article, How teachers respond to student questions when engaging in coding activities, Mr. Floyd explores a few scenarios that impact on student-driven problem-solving in coding activities. Zhang Illustrates the circular nature of the use-edit-CREATE cycle, where the purpose of “use” could constantly be at play as in creating and refining students’ computational thinking. Brodie, Albert and Chan in an article on Open and Creative Coding explore the ways in which open coding supports creativity among learners. In their article on Coding Buddies and Intergenerational thinking, Dickson, Harris, Boyd and Kotsopoulos, illustrate the ways in which computational learning plays out differently at different grade levels when taught separately and when combined. In a dialogue by Khan and Rudakoff, the construct of computational disposition is explored.
Immaculate Kizito Namukasa is an associate professor of education at Western University in Ontario and distinguished as a teaching fellow with the teaching support center at Western University, 2017 to 2020 based on her work on pedagogies incorporating maker activities in teaching. She is a past journal editor for the Ontario Mathematics Gazette – a magazine for teachers and educators and a current editor Math + code ‘Zine. For more information see http://bit.ly/IKNamukasaWesternEducation.