Betty R Zhang

“Can students learn something about coding by simply using codes?” The answer was simply, “No.” Even though the conversation did not end there, that was the first reaction of a high school computer science teacher to my question. From my personal experience, that response reflects the opinions of teachers and scholars who are familiar with computation thinking and coding. In most scholarly writings, people mainly celebrate the complexity of codes created as if it is the only means of demonstrating learning, process, result, and computational thinking. In the Bloom’s Revised Taxonomy (that is often referred to when differentiating questions into knowledge, understanding, apply… evaluate and create questions), “create” was crowned the highest level of thinking (Krathwohl, 2002, p. 215) but that does not negate the importance of the previous five levels of thinking. Students can easily and effectively develop all the other five levels of thinking if they are encouraged to understand how the codes work while using them. However, students’ impressive codes and the process of creating them often steal the spotlight and divert attention away from their fruitful first encounter with coding. I personally think we are not giving the “use” in the use-edit-create cycle enough credit for its benefit in increasing students’ exposure to and fluency in programming.

The Initial Stage of Learning

“Use” or “play” is always the first step to learning a new software program no matter the age of the learner, the final objectives, or the complexity of the program. I had no knowledge of coding, but I slowly learned coding through George Gadanidis’ (2015) eBook called Coding for Young 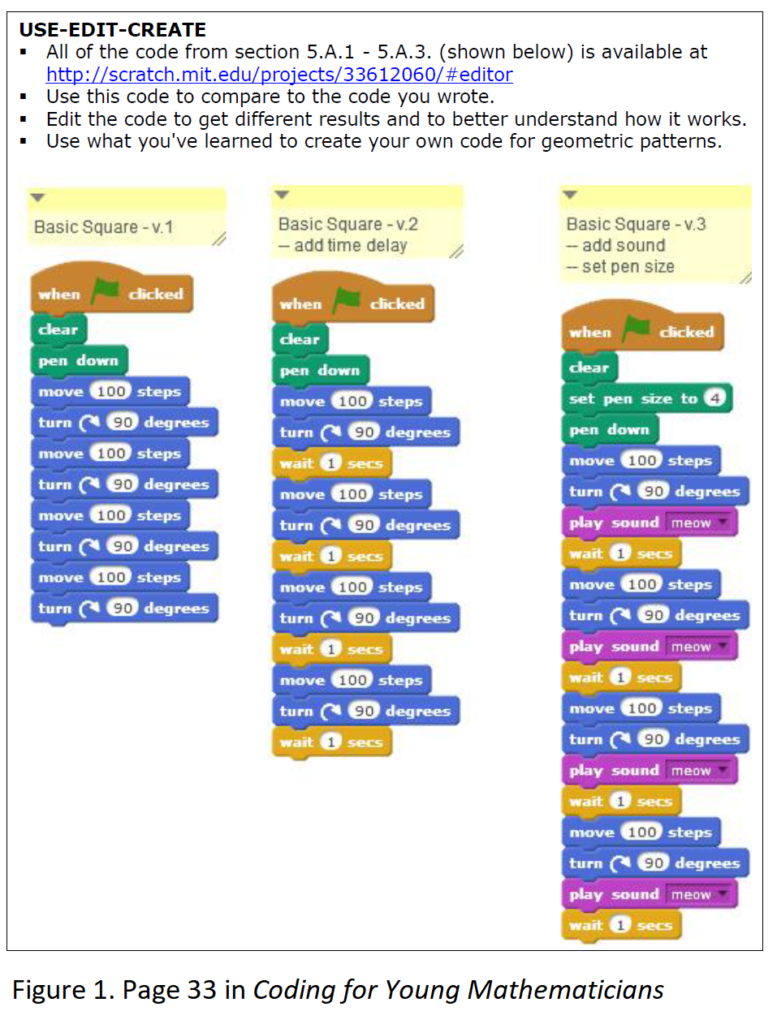Mathematicians. Gadanidis denotes “‘use’ as the using and studying of other people’s codes, ‘edit’ as editing and borrowing from existing codes, [and] ‘create’ as creating their own codes” (p. 2). “Use” helps you see how code works and that was exactly what Gadanidis encourages the reader to consider doing when using Scratch and Python at the beginning of their coding journey. The book offers different activities with step-by-step instructions, explanations, screenshots, and links to existing codes to assist new coders along. It had alleviated coding-induced anxiety because it was very easy to follow, understand, use, and recreate. Without the pressure of creating my own, I would analyze different components of the code, deconstruct it, and modify the input to observe changes in output in order to understand the scripts. Even though the artist in me always desired to create something original with my newly obtained skill and knowledge after every unit, I saw the inseparable, dependent, and recursive relationship between use, edit, and create. Unfortunately, the use-edit-create cycle seems to be interpreted by many as a linear sequence, use-edit-CREATE, where the purpose of “use” is been reduced to a steppingstone so students can quickly graduate from playing with existing codes to create their own. However, being a cycle, it is circular which means “use” will constantly be at play. It is a continuous improvement process aimed to deepen students’ interest in creating their own and refining their computational thinking.

Use = Low Floor, High Ceiling, Wide Walls

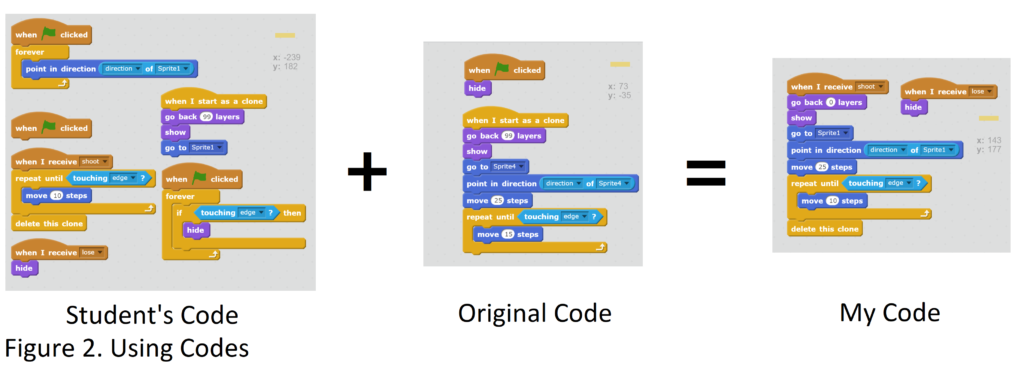
The “use” step is crucial to the implementation of “low floor, high ceiling, wide walls” teaching methodology because it exposes us to a wide range of programs and can effectively remove the initial anxiety that turns many people away from exploring coding further. Although edit-create is the natural progression from using and studying codes, “use” helps us access codes with complexity beyond our current skill levels. A Grade 7 student in a colleague’s class emailed his modification of an existing shooting game to me. I was highly intrigued, but my lack of video game skills meant I could not pick up the controls easily. I looked at the lines of his code to connect the keyboard keys to their corresponding functions in the game and I was able to move the main character through trail-and-error.  I could not, however, get it to fire any bullet with any weapon. I followed the link on the student’s coding project page to the original game and compared the scripts between the two on the controls of firing. I fixed the student’s code by simply modifying parts of the original code to fit his command language that triggers the movement of the bullet sprite. Without creating anything of my own, I gained valuable insight and knowledge on what first person shooter game entails by using and analyzing existing codes. With my minimal coding skills, I would never be able to grasp something so complex purely through “create” but it was easily achieved through “use”. I have refined my computational thinking, learned incredible codes beyond my expectations, and amplified my interest in programming through simply using and studying existing codes. This is one of the main reasons why the programming community highly
encourages sharing, using, and remixing existing codes. Scratch and Python have an enormous online library, sharing, and remixing functions to promote collaborative coding.

Application of Coding in Grade 12 Data Management

As more functions became part of my coding vocabulary, I felt more comfortable navigating through complex codes and other programming languages. This increased my confidence levels allowing more opportunities to explore the application of coding in the demanding high school curriculum. Research and activities that promote the incorporation of coding and computational thinking often halt at the doors of high school. I wanted to break the barrier and bring this valuable tool of explorative computational learning into Grade 12 math classes to tackle problems that have been troubling students for decades.

In many Grade 12 Data Management course, two units are often placed strategically at the beginning of the year to “help” students realize that they will not pass the course so they can drop it early in the school year. These two units are permutation and combination. These two closely related topics are always taught consecutively rather than concurrently, so most students have trouble deciphering which scenario corresponds to which counting method. I have witnessed firsthand the havoc and confusion these two topics have caused in my colleague’s classes that resulted in more than 15 students dropping the class. I believe the dire state can be reversed if students can approach permutation and combination simultaneously through the using of codes that provide instant feedback.

Using Python to Learn Permutation and Combination

Unfortunately, when I searched through Scratch’s library I couldn’t find good codes that illustrate the combinations of n choose r, so I expanded my coding horizon. I ventured into Python’s online resource centers. The easy transferability of computational thinking and programming skills meant I could quickly familiarize myself with Python’s language and syntax, especially when the focus is not to ‘create’ but to ‘use’. I found an entire page created by Raju Varshney dedicated to permutation and combination, and I designed an investigative activity around the using of his codes called “Can You Count?”. The first part of the activity requires students, with or without knowledge of programming, to determine the definition and application of permutation and combination through the using of provided codes and analyzing their outputs. Instead of giving them the definition at the beginning, I wanted the codes to show them the subtle yet crucial difference between permutation and combination. Even though I did not get the opportunity to run the activity with Grade 12 students, a Grade 7 and 8 split class took on this challenging task.

The codes created by Varshney are simple to follow because Python allows the creator to embed comments coloured in green within lines of code to explain the purposes of each function without disrupting the overall function. Most of the students were familiar with Scratch but had never seen Python before, yet they quickly picked up the new language with the comments and started to use the codes. Their initial response to the encounter of unknown codes was to run the existing codes without changing the input to observe the outputs. Some of them were quick to discover that even the inputs were different between the two codes for permutation, one was ([1, 2, 3]) whereas the other was ([1, 2, 3], 2). They compared the outputs and concluded that the former was changing positions of all three numbers while the latter was choosing and rearranging only two out of three. Once they understood the functions of permutation, some of them began to alter the input to permutations([1, 2, 3, 4], 3) to see if the output would reflect the changes while some scrolled down to play with combination.

For those who moved on, they first ran the existing codes without changing the input which were conveniently designed to be the same. Many did not observe the subtle difference between Permutation([1, 2, 3]), 2) and Combination([1, 2, 3]), 2) at first until they used the second combination code which changed the order of the input to [(2, 1, 3), 2]. There was added confusion with many students wondering why the author would repeat the same code? They then looked more closely at the outputs and thought “maybe (2, 1) is not the same as (1, 2)”. The idea that these differences between the order of the output and the number of outputs could be important triggered a “wait, wait, wait” moment in four students from three different groups. They began to theorize the reasons behind these strange occurrences and two of them began to converse across the room to compare their observations and reasoning. Their thoughts were scattered and permutation and combination were still foreign concepts, but they started to systematically alter the inputs and took notes on the outputs in order to confirm their suspicion. Many students could arrive at the conclusion that combination will produce less outputs than permutation even with the same input because order does not matter. For example, (1, 2, 3), (1, 2, 3), and (2, 1, 3) are three outputs in permutation but are considered the same in combination.

Then we looked at word problems in the activities in “Can You Count?” to see if the class could decide which method of counting is appropriate to use to solve the questions. To my excitement and amazement, they picked up on the small alteration in the wording and accurately determined whether it is permutation and combination. With the using of codes, a group of middle school students had learned permutation and combination, a topic that has haunted many Grade 12 students, in less than 50 minutes. Although we had only unearthed the first layer of the unit on counting, it was a promising breakthrough and a start of something new. The students were not required to edit the codes or to create their own, but they gained both mathematical knowledge, exposure, and understanding of another powerful programming agent through “use”

If the students are simply using codes to solve problems without developing their computational thinking and coding skills, then “use” loses its major educational value. “Can You Count?” was designed as a Grade 12 investigative summative assignment so it could be easily implemented in Data Management classrooms. The questions, sequence of the activity, and the rubric of this assignment were mindfully composed to show that collaboration and communication, coding and computational thinking, and critical problem solving take precedence over application of textbook knowledge. The purpose and implementation of coding embedded activities will determine the value of “use”.

Conclusion

Students learn irreplaceable lessons through editing and creating codes, and the same is applicable to using codes. The sparking and kindling of students’ interest in coding is highly dependent on the accessibility of their initial encounter with coding and subsequent usage. Using codes will, in itself, act as a gateway to programming and some students will jump immediately into editing and creating, but the more reserved students would prefer to study the codes to increase their comfortability more before changing up the codes. It will allow them more time to build up confidence while still expanding their realm of computational thinking and learning how to code. It is also easier to incorporate into everyday classes because the time it takes to choose a code for students to investigate is exponentially less than it takes for students to code something of their own. It is especially useful in high school when curriculum is demanding and cross-curricular activities will not earn students an extra credit in another subject. It is essential to note that the three stages of the use-edit-create cycle should not be placed in a hierarchical order because then the circle breaks down into a linear sequence with an ultimate end.

References

Gadanidis, G. (2015). Chapters 5. Coding for Young Mathematicians. Toronto: Canada: Brainy Day.

Krathwohl, D. R. (2002). A Revision of Bloom’s Taxonomy: An Overview. Theory into Practice, 41(4), 212-218. Retrieved February 5, 2018.

Betty Zhang is a new teacher with two years’ experience teaching in the UK near London. Now back in Canada, she is pursuing a Master of Professional Education (MPED) degree in mathematics curriculum.