by Bronna Silver – Grades 2/3 teacher, TDSB
There’s more to symmetry
Symmetry is not as simple as it first appears. It is much more interesting!
It’s more than just looking at a heart-shaped image and drawing a vertical line that divides it in two identical halves.
My students and I looked at symmetry as a transformation: as a transformation that leaves an image unchanged.
We were surprised
Although the initial intent for this lesson was to explore the “big idea” that a symmetry is a “special” transformation, we were all surprised by how many math concepts, strands, applications, and problem solving strategies we explored. Our shared goal and schema (shared knowledge) became a foundation for us to fearlessly explore math far beyond a few specific expectations and without boundaries.
Every student was able to grasp the intended concept but most were intrigued to grasp mathematical discoveries in geometry (shapes, transformations), numeracy (fractions of turns, negative turns), probability (considering all possible outcomes), measurement (angles) and pattern/algebra (patterns, organized lists).
Following the lesson, one student could not stop saying, “This was so much fun! Math really is magical, don’t you think?”
A symmetry puzzle
We started with this puzzle of a before-and-after image of a square: How did the square change?
Using their own squares made of card-stock, my students explored the different ways the square might have changed, yet still look the same:
- maybe it turned a quarter turn?
- or half a turn?
- or maybe it flipped horizontally?
Using coding
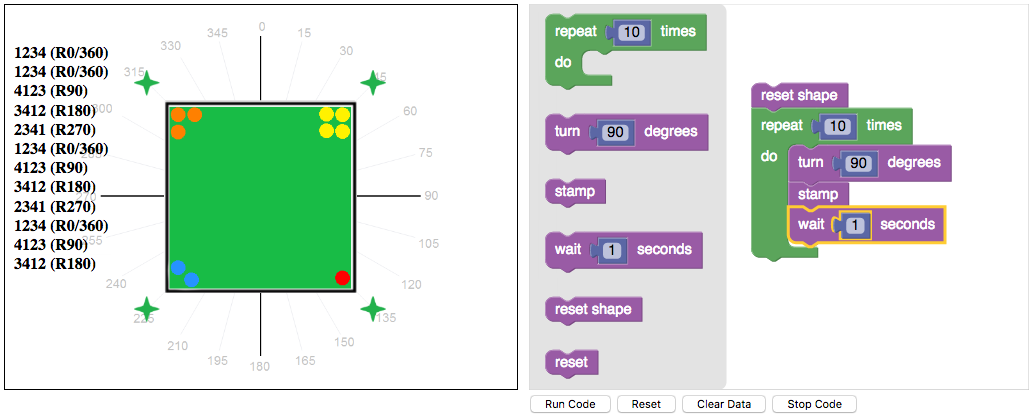
Using a coding app, they paired up to explore various rotations of the square on Chromebooks.
Permutations
The square had 1, 2, 3, and 4 dots in its vertices.
As the square rotated, the order of the vertices changed, and the new order was recorded.
We wondered how many different ways there are to order the numbers 1, 2 ,3 4. Mathematicians call such combinations “permutations”.
First we found all the permutations that start with 1. Then with 2. And so forth.
Four groups of six make 24 permutations
Why do we only get 4 permutations when we rotate the square?
- 1234
- 4123
- 3412
- 2341
One of my students suggested: “When the square turns, its vertices don’t switch places. So we can’t get them all.”
More coding
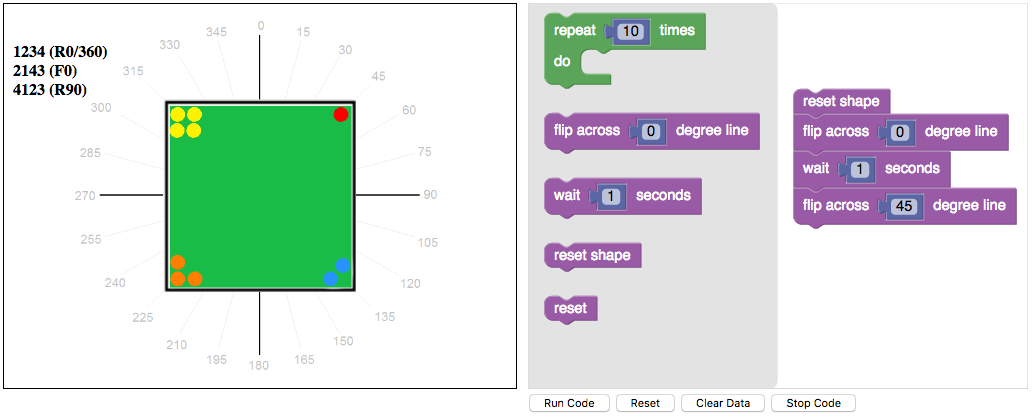
We also used the coding app to explore reflections.
Using a list of all 24 permutations, students circled the rotations and underlined the reflections.
Combining transformations
Some students noticed that when they combined rotations, the result was always another rotation.
But when they combined reflections, sometimes the result was a reflection and sometimes a rotation.
For example, one of my grade 2 students noticed that a reflection across the 0 degree line
followed by a reflection across the 45 degree line
was the same as a rotation of 90 degrees.
“Math is so cool!” he said.
I found it interesting that although the coding app was strictly mathematical, my young students were interested and engaged.
Our class song
This is the song we wrote about our experience.
Lesson resources
Click on the links below for more resources.