Chantal Buteau & Eric Muller, Brock University
Yes, mathematicians (pure and applied) do it. Not all of course, but many of them. The European Mathematical Society (2011) recently acknowledged this emerging way of using coding for mathematical-based research:
Together with theory and experimentation, a third pillar of scientific inquiry of complex systems has emerged in the form of a combination of modeling, simulation, optimization and visualization (p.2).
Also in 2016, mathematicians who led a six-month long thematic semester on Computational Mathematics in Emerging Applications at Centre de Recherches Mathématiques in Montreal indicated that:
A fundamental change is taking place in the role of applied and computational mathematics. The relationship between the modelling, analysis, and solution of mathematical problems in applications has changed… In emerging applications, the choice of models goes hand in hand with the computational tools and the mathematical analysis.
So, mathematicians do it. What is exactly the ‘It’? We turn to the work of Weintrop et al. (2016) to obtain more details of the use of coding, more generally of computational thinking, in mathematicians’ work. They propose that ‘It’ includes four kinds of practices: data practices (data collecting, manipulating, visualizing, etc.), modeling and simulation practices (model designing, using to understand concepts, etc.), computational problem solving practices (preparing problems for computational solutions, choosing effective tools, developing modular solutions, etc.), and system thinking practices (investigating a complex system as a whole, thinking in levels, etc.).
As it turns out, they’ve discussed how these four kinds of computational thinking practices can be realized in the mathematics and science high school classrooms (see the title of their paper!) And we say, in the university mathematics classroom too!
Indeed, since 2001, Brock University mathematics majors and future mathematics teachers learn, through a sequence of three programming-based mathematics courses, to design, program, and use interactive computer environments in order to investigate mathematics concepts, conjectures and real-world applications:
Readers who are interested in getting some more details about these three courses, called Mathematics Integrated with Computers and Applications (or MICA for short), may look at (Buteau, Muller, & Ralph, 2015) or contact us. Note that as of this year, MICA III is now split into two courses, one for math and science majors and one for prospective math teachers, whereas the latter aims at preparing them for the integration of computational thinking in the school classroom.
Let’s see an example of a lab activity from the first-year MICA course designed for students to use loops and if-then-else structures. At this point in the course, for most students these programming concepts are new. The guided task below is to create a program to check whether a positive integer is prime or not. This eventually leads to students’ first individual assignment of designing, coding and using a program to investigate a conjecture of their choice on prime numbers. Such an assignment contains a written report summarizing a student’s investigation.
Each of the three MICA courses end with original programming-based math projects (done individually or in pairs) for which the topic is selected by the students themselves. This is an opportunity for students to engage in a math project that is meaningful to them. Here are three examples of such student work.
A pure math project done by second-year Adam Profetto for the investigation of inner-symmetries of the (generalized) Mandelbrot Set.
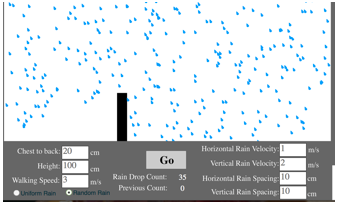
 A real-world application project done by second-year Kylie Maheu and third-year Matthew Lillie to investigate whether it’s better to walk or run in the rain (do you know?)
A real-world application project done by second-year Kylie Maheu and third-year Matthew Lillie to investigate whether it’s better to walk or run in the rain (do you know?)
 A teaching project done by first-year Lindsay Claes for the guided learning of the Pythagorean Theorem (Grade 10).
A teaching project done by first-year Lindsay Claes for the guided learning of the Pythagorean Theorem (Grade 10).
 We have studied different aspects of this sustained MICA implementation at Brock University. For example, student learning (Buteau et al., 2016); competencies developed by students (Buteau, Muller, & Marshall, 2014); assessment of coding-based math projects (Buteau & Muller, 2016); pedagogy (Buteau & Muller, 2014); etc.
We have studied different aspects of this sustained MICA implementation at Brock University. For example, student learning (Buteau et al., 2016); competencies developed by students (Buteau, Muller, & Marshall, 2014); assessment of coding-based math projects (Buteau & Muller, 2016); pedagogy (Buteau & Muller, 2014); etc.
Our experiences in developing and teaching these math + coding courses together with our research suggest that our university students are indeed engaging in doing mathematics with coding in a similar way as mathematicians do (as highlighted in Broley, Buteau & Muller, in press). And some former MICA students seem to also agree with this:
“The MICA program truly deepened my understanding of mathematics in the current world. This understanding has been beneficial to me in my work with secondary students as I can explain how mathematical modeling is applicable to the world around them and even help them with the basics of modeling real-world phenomena using computer-based applications.” (Jessica, now a high school mathematics teacher and program leader)
“These courses have fostered in me the invaluable skills of being able to question and search for answers, engaging in an inquiry process, and developing programming skills.” (Kristina, now a post-secondary college mathematics instructor)
“Learning how to program and then use that skill to ‘do math’ in this new sense gave me a feeling of empowerment as a young mathematician that I had never felt previously.” (Laura, now a Ph.D candidate in mathematics)
References
Broley, L., Buteau, C., & Muller, E. (in press). (Legitimate peripheral) computational thinking in mathematics. Proceedings of the Congress of European Society for Research in Mathematics Education, Dublin (Ireland), February 2017.
Buteau, C., & Muller, E. (2016). Assessment in Undergraduate Programming-Based Mathematics Courses. Digital Experiences in Mathematics Education, 1-18.
Buteau, C., & Muller, E. (2014). Teaching Roles in a Technology Intensive Core Undergraduate Mathematics Course. In The Mathematics Teacher in the Digital Era. Springer Netherlands, 163-185.
Buteau, C., Muller, E., & Marshall, N. (2014). Competencies Developed by University Students in Microworld-type Core Mathematics Courses. In Proceedings of Joint Meeting Int. Group Psychology Mathematics Education (PME 38), Vancouver, Canada, 2014, 209-18.
Buteau, C., Muller, E., & Ralph, B. (2015). Integration of programming in the undergraduate mathematics program at Brock University. Online Proceedings of Math+Coding Symposium, London, ON. Retrieved from: https://researchideas.ca/coding/docs/ ButeauMullerRalph-Coding+MathProceedings-FINAL.pdf
Buteau, C., Muller, E, Marshall, N, Sacristán, A.I., & Mgombelo, J. (2016). Undergraduate mathematics students appropriating programming as a tool for modelling, simulation, and visualization: A case study. Digital Experience in Mathematics Education, 2(2), 142-156. (DOI) 10.1007/s40751-016-0017-5.
European Mathematical Society (2011). Position Paper of the European Mathematical Society on the European Commission’s Contributions to European Research [online]. http://ec.europa.eu/research/horizon2020/pdf/contributions/post/european_organisations/european_mathematical_society.pdf. Accessed 14 September 2015.
Mulder, A. & Chantal Buteau, C (2017). Needles, Pi(e), and Coding. Math and Code ‘Zine 2(3).
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25, 127–147.

