By Alana Mulder (prospective mathematics teacher, Brock University), with Chantal Buteau (Brock University)
One of the affordances of the computer when doing (or learning!) mathematics is the possibility of running large (well, let’s be honest, very large!) simulations. With coding, one can design such a simulation with a specific aim in mind. And I had something in mind: dropping needles on a floor and estimating the likelihood it would touch a floor crack. I’m actually cheating with this idea, since my prof put this idea in my mind; that is, this simulation was an assignment last winter in my third coding-based mathematics course. Regardless of the origins of the idea, I had a lot of fun developing and running the simulation. In fact, when working on this assignment, I even discovered an exciting math surprise! I will talk to you about this first with the help of a short play I wrote. And I will then come to the heart of this short article: a description and a reflection on my engagement in this computational thinking activity.
Needles and Pie: The Play
Characters
Alana, math student explaining the problem
Rachel, friend of Alana
Jesse, friend of Alana
The Script
Scene: in the hallways of Brock University, waiting for class to start. Alana is sitting by herself, reading math notes
(Enter Rachel)
Alana: Hey, Rachel! Come sit with me! Are you waiting for a class?
Rachel: Hey, Alana! Yeah, I am waiting for sociology. What are you working on? (sits down)
Alana: This? It’s some math stuff I learned today. It’s pretty interesting, actually.
Rachel: Really? Can you show me?
Alana: Sure! See, it’s an experiment called the Buffon Needle Problem, where we throw some needles and it can actually approximate Pi—
(Enter Jesse)
Jesse: What’s this I hear about pie? I love me some pie.
Alana: (sighs) Not that kind of pie, Jesse…
Jesse: Then what kind of pie? Apple is my favourite.
Alana: No, no, the math kind.
Jesse: I’ve never heard of that flavour before.
Rachel: You know, 3.14…?
Jesse: Oh, right. That kind of Pi doesn’t taste very good.
Alana: No, but it’s very interesting! And I can approximate the value of Pi by throwing needles!
Jesse: That sounds unsanitary, not to mention a little farfetched.
Alana: Just hear me out. I’m explaining it to Rachel, you can listen too.
Rachel: Yeah, Jesse, listen.
Jesse: Okay.
Alana: Right! So, there’s this math problem: if I throw a needle on a slated floor, what is the probability that the needle will cross a crack?
Rachel: Wouldn’t that depend on the length of the needle?
Alana: It does! For our problem, we assumed that the distance between the two slates is 1 unit long, and the length of the needle is ½ units.
Jesse: I’m still not seeing where pie of any kind, math or otherwise, comes into play here.
Alana: Here, let me show you…
Alana presents the following diagram
Alana: If the distance y from the center of the needle to the closest crack is less than the distance from the center of the crack to the endpoint of said needle, which is given by y<=1/4sin(theta), then the needle crosses the crack!
Rachel: Okay, I see how that works, but I’m still not sure how that gives us an approximation of Pi.
Alana: Well, the needle can fall at any distance of the closest crack and with any angle, right? That means any distance between 0 and ½ and any angle between 0 and 180 degrees (which is Pi), right? From this we can determine the theoretical probability of a needle crossing a crack by modeling a needle drop through a distance y and an angle . The probability is calculated as the area under 1/4sin(theta) (i.e. when the distance y is less than the end of the needle), divided by the total area modeling a needle throw [It’s the [0,Pi] x [0,1/2]-rectangle]. By using Calculus [Integrating the function], we get the probability the needle will cross the crack in this case is 1/Pi.
Jesse: How do the needles still have anything to do with this? If I throw a bunch down, how would I get some approximation of Pi?
Alana: Well, the theoretical probability is roughly the empirical probability.
Jesse: Sorry, what does that mean?
Alana: It means that if I run a computer-generated simulation throwing down as many needles as I want on a slated floor, the empirical probability that a needle will cross a crack will be about 1/Pi, our theoretical probability.
Rachel: Oh my gosh! I get it now!
Jesse: You do?
Rachel: Yeah! If the computer program generates the probability that a needle will cross a crack to be roughly 1/Pi, then all you need to do is take the inverse of that number and you get an approximation of Pi!
Alana: Yeah! You get it!
Rachel: Wow, that was really interesting! Thank you for sharing that with us.
Alana: No problem!
Jesse: I actually understand it! But all this talk of Pi has made me pretty hungry…
Alana: (laughs) Of course it has, Jesse. (shakes head in amusement)
Rachel: (laughs) Well, I have to go to class now. I’ll see you guys tomorrow?
Jesse: Yeah, I’ll see you then. I have to go to class too.
Alana: Same here. Bye, guys! Thanks for listening to my math stuff!
Exeunt
Needles and Pi: Coding the Simulation
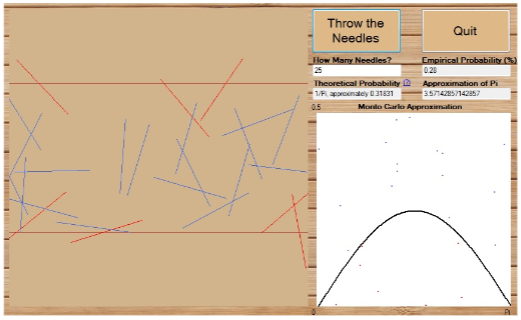
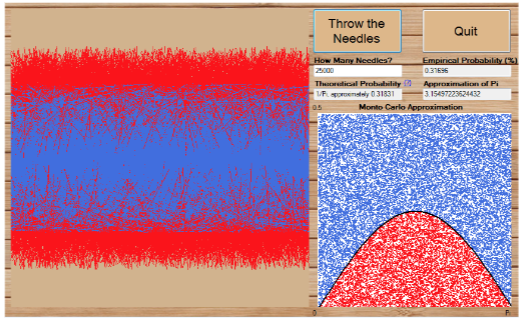
Our assignment, from the mathematics course called “Visual and Interactive Mathematics”, concerned the Buffon needle problem: if a needle is randomly dropped onto a slated floor, what is the probability that it will cross a crack in the floor? We saw in lecture that this problem can be solved as a geometric probability problem, which means that it can be modeled as certain areas, given the assumption that any points are equally likely to happen. My professor proposed we create a program that simulated the problem through two different visualizations; namely, depicting the needles on a slated floor, and also as points (theta,y) in the [0,Pi] x [0,1/2]-rectangle, in order to estimate both the probability the needle crossed a crack, and an approximation for Pi. In this simulator, the proportional area under the curve 1/4sin(theta) in the rectangle was approximated using the Monte Carlo approximation method: generate n random points in the rectangle, the proportional area is approximately the ratio of the number of points under the curve over n, the total number of random points. Let me show you the simulator I created:
Play around with it first with only a few needles, then go wild (that’s what I did)! Do you notice how the approximation of Pi gets more and more accurate as the number of needles dropped on the floor increases?
Not having coded in VB.NET for nearly one year (not since the second-year coding-based math course called Mathematics Integrated with Computers and Applications II, or MICA II for short), this assignment served as a refresher of our vb.net coding skills involving, for example, the use of variables, loops, conditional structures, functions, and skills to graph (which in vb.net needs to be coded). In MICA I, we had learned vb.net programming for the purpose of conducting mathematical investigations or applications. In MICA II we had applied that method in more complex mathematical contexts, yet with some considerable guidance in the first steps to prepare the coding of the mathematics simulators. In this third-year course newly designed this year for prospective mathematics teachers such as myself (the original MICA III course is now split in two sections – one for prospective teachers and one for math and science majors), we were given little to no guidance with the initial steps: we had to engage in full problem solving.
If you are interested in hearing more about the MICA courses, see Buteau & Muller (2017) or Buteau, Muller & Ralph (2015).
Reflecting (While Eating Pie): It Was a Computational Thinking Activity
As part of the assignment, we were asked to reflect on our learning experience from the perspective of computational thinking. We had discussed what computational thinking means; for example, the definition from Cuny, Snyder and Wing (2010): “The thought processes involved in formulating problems and their solutions so that the solutions are represented in a form that can be effectively carried out by an information-processing agent.” (p.1)
We also discussed affordances of computational thinking for mathematics learning; for example, based on a study in a Grade 1 class, Gadanidis et al. (2016) elaborated on seven affordances. In the following, I discuss my experience with the Buffon needle assignment, and how, through coding, I engaged with these seven affordances (in a post-secondary context). When I began, I was happy to find that an advanced knowledge of mathematics was not required for the exploration of this experiment. Since the math was relatively simple, I could focus more on the creation of the code. Once I was able to abstract how to measure whether my computer-generated needle crossed a crack, the program was relatively simple to create. Through automation and dynamic modeling, I worked through the iterative process of creating my code to determine whether a needle did indeed cross a crack. First, I determined which crack the centre of the needle was closest to, and then checked whether that distance y from the centre of the needle to the crack was greater than the vertical distance from the centre of the needle to its endpoint. That is, whether y>1/4sin(theta), where is the angle from the centre of the needle against a horizontal line. If y is larger than the vertical distance, the needle does not cross a crack; if y is smaller or equal to the vertical distance, the needle does cross a crack. With this simple idea, I was able to create a program that explored the Buffon needle problem and created an approximation of Pi, which overall I refer to as a low floor, high ceiling characteristic of this task.
However, despite my solution being correct, there was a simpler approach to solving the problem. Instead of measuring the distance from the centre of the needle to a crack and comparing that to y>1/4sin(theta), I could just have examined the endpoint of the needle to see whether it exceeded a crack. For an extension of the Buffon needle problem, where instead of throwing needles on a slated floor I created a program that threw them on a tiled floor, this was the approach I took. By examining the end points, it saved unnecessary calculations. With this approach, I could imagine exploring with different shaped tiles (triangle, rectangle, etc.) but the course was moving on to other assignments and that remained an idea only. This is a testament to the wide walls nature of the problem. There is more than one approach to creating a program to solve the problem, and it all depends on the individual and how they understand the experiment, and then possibly build on it. Additionally, I was not told by my professor how to solve the problem, but instead was given free reign to approach a solution that made most sense to me. Since I had this level of control over the approach and design of the program, there was a true sense of agency in the design process.
When this problem was proposed to the class, it was done in two stages. First, my professor explained the Buffon needle problem and sent us to work on creating our programs. Only later did she highlight to us the connection of this experiment with the capability to approximate Pi. Once I implemented the Monty Carlo approximation method in my program, I could see with own eyes this conceptual surprise. It was so shocking to me that an experiment with needles on a slated floor had the power to approximate the value of Pi. In fact, I was so surprised and fascinated with this realization I went home and told my roommates about the problem and showed them my program. Additionally, being able to model, see and show the experiment created a sense of tangible feel. I could easily see and explain how the program was working when I generated only a small number of needles, and then when I increased their numbers, the approximation of Pi became more accurate.
I strongly believe that my engagement and enjoyment from this assignment would have been lost if it were a standard paper-and- pencil experiment. Imagine trying to throw the necessary number of needles by hand and attempting to count them one-by- one to gain a moderately accurate approximation of Pi. The excitement of the results would be lost in the tediousness of having to count the needles! However, constructing this experiment as a programming assignment allowed me to gain a fuller, more comprehensive understanding and appreciation towards the Buffon needle problem while experiencing many affordances from computational thinking.
References
Buteau, C. & Muller, E. (2017). Coding + Math at University: Just like Mathematicians Do It! In Math+Code’Zine, 2(3), May 2017.
Buteau, C., Muller, E., & Ralph, B. (2015). Integration of programming in the undergraduate mathematics program at Brock University. Online Proceedings of Math+Coding Symposium, London, ON. Retrieved from: https://researchideas.ca/coding/docs/ButeauMullerRalph-Coding+MathProceedings-FINAL.pdf
Cuny, J., Snyder, L., & Wing, J.M. (2010). Demystifying computational thinking for non-computer scientists. Unpublished manuscript. Cited in: https://www.cs.cmu.edu/~CompThink/resources/TheLinkWing.pdf
Gadanidis, G., Hughes, J. M., Minniti, L. & White, B. J. (2016). Computational thinking, Grade 1 students and the Binomial Theorem. Digital Experiences in Mathematics Education, 1-20.