Steven Khan & Sally Rudakoff
This article is presented as a research informed dialogue between the two authors. It represents a reconstruction of conversations that occurred over several weeks, in person and via email as we explored the affordances of a wooden puzzle game for scaffolding understanding of the process of decomposition as used in computational thinking (CT) frameworks and computational dispositions in the early years alongside academic readings. We have not identified either one of us as S1 or S2. For the purpose of a more coherent dialogue we have blended thoughts and ideas together.
S1: We both work with teachers in some way and I notice that some teachers are struggling with really appreciating the difference between computational thinking processes and coding as a literacy and of course how it relates to their curriculum. I know there is going to be some reference to computational thinking and coding in the new curriculum that might be coming. I’m hoping if we focus on the computational thinking (CT) skills in the elementary grades that students will begin to develop skills and concepts that will follow them as they advance through our school system.
S2: I agree. I’ve come across this term – proto-computational thinking (Tatar et al. 2017) – that I think might be a more realistic and achievable systemic goal for naming what we do at the earliest grade levels in a way that is intellectually honest and respectful of the multiple responsibilities around learner competencies that teachers are already accountable for developing.
Critical aspects of computational thinking
S1: It’s like the Mathematical Processes or Standards of Mathematics Practice with teachers new to this area – it seems difficult in practice for many teachers to make necessary distinctions between the concepts and draw appropriate connections among them as to how the concepts relate to one another.
S2: “It’s as if they don’t have sufficiently diverse, haven’t connected or aren’t able to call upon grounding or foundational experiences at the appropriate times that would allow them to extend their understandings and really discern the critical aspects of these concepts as needed for teaching.”
S1: “Critical aspects?”
S2: “Sorry. It’s a concept from Ferrence Marton’s book on Variation Theory of Learning (2014). His main argument is that learning is a function of discernment, or the coming into conscious awareness of an object, relation, concept or phenomenon of which one was not previously consciously aware. The aspects of the thing one is trying to learn — called the object of learning in Marton’s variation theory — or have a learner notice and become aware of, is referred to as the critical aspect. So, for example, one could say that in Hoyles and Noss’ (2015) framework for computational thinking, there are 4 critical aspects — Pattern Recognition, Decomposition, Abstraction, and Algorithm Design — to be discerned and developed by the learner with the help of the teacher and the learning materials.”
Dispositional aspects of computational thinking
S1: “Thanks. I’ll read up some more on it later. And then there’s the dispositional aspect which refers to, “the willingness and opportunity to make use of knowledge and ability” in the area of CT (Pérez, 2018, p. 427). In the paper I read by Pérez (2018), he argued that students will need to develop CT dispositions if they are to derive benefit from meaningful computational thinking learning opportunities presented in classrooms in mathematical contexts and that if students are able to recognize CT opportunities on their own, they will then be able to “recognize, respond to, and appropriately act” on these opportunities (Pérez, 2018, p. 428). But what can we use to provide those opportunities?
S2: “Kids love games! Teachers and parents generally love playing games with young kids. I’m wondering whether you could you develop foundational computational thinking skills with commercially available children’s tabletop games?”
S1: “Well there’s already a number of games out there such as robot turtles, little coder, code monkey island, coding farmers, coding is good and the list grows annually.”
S2: “True, but all of those more or less already have coding in the name so that’s too obvious and might scare off some teachers.
S1: “True. The lure of game play might not be enough to overcome the fear and anxiety around the terms coding and computational thinking processes.”
S2: “I wish we had just one game we could use as a test case to think through and with about this.”
S1: “That’s a great idea.”
Discerning Decomposition & Recomposition
S2: “Have you ever played with a game called Archelino?”
S1: “No. I haven’t what’s it about and who is it for? Is it fun?”
S2: Well I had fun playing with it and I think there’s something about it we could use to develop a way to help teachers discern somethings about foundational or proto computational thinking ideas.
S1: “Sounds interesting.”
S2: “Here’s what the set looks like in the box. The game set consists of: 1 grooved wooden ark; 7 wooden figures (Noah and six animals), each about 5cm or two inches tall; a puzzle book containing 60 puzzles categorized as Starter, Advanced, Expert and Master; and one multilingual instruction booklet (see Figure 1). The game takes place in the context of the story of Noah’s Ark with the premise that certain animals want to be next to other animals, or want to converse with particular neighbours.”
The box says it’s recommended for ages 4 and up and typical playtime is approximately 10 minutes.
S1: “So what do players have to do?”
S2: “The puzzle cards present clues in the form of an iconic visual description of how the animals are ordered sequentially from left-to-right (1st, 2nd etc.) and how they are oriented (facing to the left or right), or whether they want to be engaged in conversation (facing each other with a speech bubble between them). The goal is to use the visual clues to solve the puzzle by placing the animals in the correct sequential order and orientation (facing to the left/right) on the ark. The instructional booklet and box art explicitly name learning to ‘think strategically’ as the main affordance of engaging with the puzzle.”
S1: “I’ve noticed that teachers and parents understand strategic thinking, but when we say logical thinking, I don’t think they see how the two are related. This is nice. Let’s try a few.
S2: “Here’s the two of the early puzzle clues. What do you notice? What do you think players might do or struggle with?”
S1: Well the first is pretty straightforward – put the animals in the right sequential order, though if students don’t know their numerals the position numbers might be distracting. There could also be some fine-motor issues getting the animals into the groove and sliding it forward with young kids. Let me try the second one myself. Ok. In this one I noticed that all the animals are paired up and facing each other. I could see some kids missing that and just ordering the animals randomly and not paying attention to which direction they were facing in the picture. It’s a nice subtle but important element. Do the puzzles get more challenging? How do they level up the challenge?
S2: Before I show you how the clues get progressively harder I want to connect what you noticed back to Variation Theory. Notice that you were able to discern at least three things, namely that the animals can all face in one direction, can face each other and can face away from each other and I noticed while you were doing the puzzle you used positional language like first, second and so on and I know that’s usually in the early curriculum and I’ve seen it in other logic puzzles in math contests. So maybe we could also make a link to using the game to provide one sort of foundational experience towards solving puzzles like that?
S1: Thanks. Yeah I was thinking about variation theory and how it might connect. But other than some really basic ideas related to sequencing here, so far I am not seeing a lot of scope for computational thinking.
Discerning Decomposition
S2: Ok. Check out the clues for these two puzzles and tell me what you notice.
S1: Oh that is really nice. I like how they’ve split up the clues and how the solution to puzzle 4 has the same structure – all the animals facing left – as puzzle 1. It’s a nice looping back, a recursive elaboration if you will (Davis & Simmt, 2003). I also notice how they’ve split the clues into two lines and then three lines, and well obviously you could do more lines.
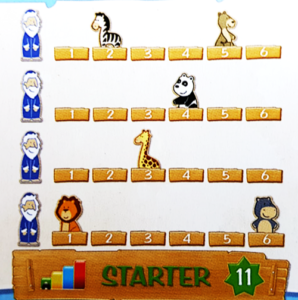
S2: Yeah. Puzzle 11 has 4 lines.
S1: You know what this reminds me of…decomposition. We know what the goal is – put the animals in the Ark in a particular order and orientation and we get these visual clues as a series of ‘instructions’ that have been decomposed to get us to the goal. I know that the ability to decompose a problem into smaller components is seen as an important aspect of both CT and mathematical problem-solving, it’s in the Hoyles and Noss framework we talked about earlier. But decomposition is also a core component of other CT frameworks, such as Computing at School’s Concepts in CT (2015) and the ISTE’s Standards for Students in CT (2016). I also know from working with students and teachers that not many teachers have had opportunities to work with explicitly decomposing problems in mathematics and in computer science and certainly in teaching students to do so. Maybe there is some potential here after all.
S2: Ok, let’s stick with just one foundational CT skill for now – learning decomposition – and think through this game some more. If other things emerge we’ll note them. But now we have a focus. What else are you thinking?
S1: Well, looking at the clues and thinking about them in terms of learning decomposition as the goal the clues present the end goal as a set of 2 or more discrete non-overlapping puzzles. Also, there’s no redundant information in any of the clues, such as placing the same animal in its correct position in more than one clue. I’m really beginning to see and value in these Archelino puzzle clues, and the gameplay, the opportunity for explorative practice (Trninin, 2018) which is, “a pedagogical approach with a high degree of guidance but minimal degree of explaining” (p.150, italics in original). It’s related to an analogy a well-regarded mathematics educator, Hans Freudenthal (1971), once made between learning mathematics, geometry specifically, and learning to swim. He observed a similarity in good teaching in both instances as the qualified teacher helping the learner come to certain sensory-motor and initial conscious awarenesses without initially offering explanations. This keeps the learner’s limited attentional (cognitive-emotional) resources on a small set of important-in-that-moment critical features. I think I see something similar going on here. I especially like how starter puzzles 7 and 11 continue this elaborative explorative practice first with an example where the problem is decomposed in a continuous piecewise manner, and then onto a situation where the animals are more unevenly distributed. But I wonder would a child make the connection that the visual image of two lines represents the same goal as before? I think that’s not an obvious discernment early on.
S2: Well, I tried it out with a 3.5 year-old and that was an issue. They thought it was going to be 2 arks, but once I explained that the goal was the same and reminded them of the position numbers they seemed to get it. But that is definitely a discernment that needs to be made here – that the multiple images in the clue relate to the single ark. I think this was the moment when they became aware that the whole visual clue could be decomposed into more than one part that was smaller. It’s somewhat different from the building instructions you find in Lego or Duplo where the construction of the final design is fully decomposed into all the algorithmic steps. Here and in some of the later puzzles you have to do the work for yourself in recomposing the problem.
Discerning Recomposition
S1: Recomposing! You know I don’t think the CT literature really talks about recomposing problems but really that is what you also need to learn to do in addition to learning how to identify where some places for decomposing a problem might be fruitful. And we already do a lot of work in number and spatial reasoning on composing and decomposing mathematical objects (numbers, shapes and solids) and also that skill and habit is used in Art, Music, Language and Physical Education so it might be a small enough safe step for teachers with less experience in this area of computational thinking.
S2: I like that. I mean decomposing problems is part of the bread and butter of mathematicians, computer scientists and programmers and getting there requires a sufficient variety of curated experience – seeing lots of different specific examples and making necessary discernments and appropriate connections among them – and persistence with individual problems over time. I think this connects nicely to what you were saying earlier about computational dispositions. What do you think?
Developing Computational Dispositions
S1: The paper I read proposed three aspects to a productive computational disposition – tolerance for ambiguity, persistence, and collaboration (Pérez, 2018). Let me see if I can connect those with Archelino.
Persistence
S1: The first aspect is tolerance for ambiguity which refers to, “a tendency to experience ambiguous situations or stimuli as enriching and engaging” (Pérez, 2018, p. 444). Certainly the images of the animals and the story setting are engaging but the ambiguity in clues such as those presented in Puzzle 4 and others does create some ambiguity that requires interpretation. This is an easily resolved ambiguity, though from what I’ve seen in some of the later puzzles the ambiguity does increase requiring more reasoning. Persistence is the second aspect and that relates to what you were saying about learning to decompose and recompose problems. For sure in the context of Archelino students would need to display task persistence as they work to successfully complete the puzzle. With Archelino, students may need numerous attempts to successfully complete some puzzles, especially as the difficulty level increases and begins to incorporate more elements. The third aspect of a productive computational disposition is collaboration and we really haven’t talked about that as yet, we’ve been looking at it as an individual game, maybe with some parent or teacher interaction and a lot of the literature on computational thinking with young kids talk about the importance of collaborative activity. Could we maybe design the play so that it could be more collaborative?
Collaborative play
S2: Sure. I think so. How about we try playing it like a barrier game with one person translating the visual clues into a set of oral instructions for the other person? Let’s give it a try with a different puzzle.

S1: Ok, here goes. The Giraffe is in the first position (bow of the boat) facing to the right. The Kangaroo is in the last/sixth position facing left. The Hippo is next to the giraffe facing the giraffe. The lion is next to the Kangaroo facing right. The Zebra is to the right of the hippo facing right. The Panda is facing the zebra. Now your turn. You try it.
S2: The Giraffe is in the first position facing right. The Hippo is in the second position facing left. The Zebra is in the third position facing right. The Panda is in the fourth position facing left. The Lion is in the fifth position facing right. The Kangaroo is in the sixth position facing left.
S1: Oh wow. That was fun. I noticed how different our strategies were. I followed and translated each line of the visual instructions similar to how I would have done the puzzle.
S2: And I looked across all the clues and used the positional indicators, similar to how I would do it for myself. That was interesting; both of our strategies lead to a successful solution of the puzzle and we haven’t actually talked about or shared our personal strategies.
S1: Yes and I like how you sequenced your instructions so that the puzzle built up from left to right without gaps. I can also see how doing this as a partnered activity in class would allow for experience with enacting different strategies and provide a teacher with an opportunity to draw out the differences.
S2: Yes. In a classroom, small group, or teacher interview setting, allowing students to see and make sense of alternative strategies such as these is important. They increase both the personal example space of strategies of which learners become aware, and increase the potential for flexibility of thinking in future puzzles.
Productive ambiguity
S1: And this definitely connects with that third aspect of a computational disposition. I noticed I really had to listen attentively and carefully as you were speaking and I had to attend to both the position and the orientation. In a whole class setting deliberate and intentional sequencing of the sharing of important variations in strategies might also provide students with opportunities to experience situational ambiguity (Pérez, 2018) and make connections as they discuss possible solution pathways.
S2: I also like how this task as a partnered collaborative activity could be made more or less challenging depending on the degree of specificity of the oral instruction used and whether or not the concepts used were shared. I can certainly see opportunities for what let’s call productive ambiguity, sort of an analogue to productive struggle, which might require them to deal with the ambiguity in finding ways to reduce it by asking clarifying questions for example. For example, we could also have said, the animals are arranged in pairs facing each other, there is an AB repeating pattern or that animals placed on odd-numbered spaces are facing right, and animals placed on even-numbered spaces are facing left. I love how many ways there are to talk about this simple puzzle.
S1: Yes I see a good opportunity here for younger learners to work on and see the value of precision in their mathematical communications. It provides a nice space to experience that productive ambiguity and to have to work to resolve communicatively, mathematically and computationally ambiguous situations that are non-threatening to build students’ confidence and questioning skills when faced with challenging cognitive tasks involving decomposition. I find strong resonance in this approach with a discussion of the benefits of teaching computational thinking through embodied experiences, which allows for hands-on learning (Sung, Ahn & Black, 2017). In that study they found that, “[c]hildren who were asked to provide commands to a surrogate by decomposing steps to solutions developed robust learning and improved their number line estimation” (p. 459). I really like what we’ve talked about so far. I think that the existence of a number of different valid ways to approach the problem depending on what is noticed and attended to and the opportunity to bring in a variety of mathematical ideas is a character of a good low-floor task for elementary learners and teachers. I can see how working with young students and explicitly teaching this important construct of decomposition and precision can help students to notice, name and nurture computational thinking opportunities in their later studies. I can see how it might contribute to developing a healthy computational disposition.
Is it worth it?
S1: I’m wondering if this is really worth it. You know most schools have tight budgets and little wiggle room and we wouldn’t want to be offloading costs directly onto teachers. I checked online and it currently retails for $29 on Amazon.ca and $25.00 on FoxMind.com. That’s not too bad unless you wanted to have multiple sets for a classroom or school.
S2: True. Some teachers already use part of their paycheck to buy materials. I think of it as an investment in the classroom as with many durable wooden resources for early learners for example, traditional Montessori and Waldorf materials, price can be an access barrier for individuals, schools, boards and districts. At the same time, we both work in organizations that have developed and maintain libraries that loan materials such as games, puzzles and technological devices, and I think the free public library system also enables teachers and parents to access similar resources through requests and delivery to their local community branches. Really, the most valuable aspect of the set is the puzzle cards and you could create lots of similar puzzles using similar materials that kids or teachers have on hand.
S1: That’s true, we could easily substitute other more readily available and affordable artifacts such as connecting cubes, solids, pentominoes, stuffed animals and recycled plastic figures for the animals in this set. But I also think there is good value in parents and pre- and in-service teachers spending time thinking about the way the puzzles are sequenced if they wish to remix this game using different materials or scenarios.
End
S2: This was a really interesting experiment. And I’m sure there’s additional connections we could make if we kept at it. Do you think anyone else would find our conversation interesting?
S1: I think so. Let’s write something up and see what happens.
References
Computing at School (2015). Computational thinking: A guide for teachers.
http://community.computingatschool.org.uk/files/6695/original.pdf
Davis, B. & Simmt, E. (2003). Understanding learning systems: Mathematics education and
complexity science. Journal for Research in Mathematics Education, 34(2), 137-167.
Freudenthal, H. (1971). Geometry between the devil and the deep sea. Educational Studies in
Mathematics, 3, 413–435.
Hoyles, C., & Noss, R. (2015). Revisiting programming to enhance mathematics learning, math
+ coding symposium Western University. London, Ontario, Canada: Western University. https://researchideas.ca/coding/proceedings.html
International Society for Technology in Education. (2016). ISTE Standards for Students.
http://www.iste.org/standards/standards/for-students-2016
Marton, F. (2014). Necessary conditions of learning. Routledge.
Pérez, A. (2018). A framework for computational thinking dispositions in mathematics
education. Journal for Research in Mathematics Education, 49(4), 424-461.
doi:10.5951/jresematheduc.49.4.0424
Rich, K.M., Strickland, C., Binkowski, T. A., Moran, C. & Franklin, D. (2017). K-8 Learning
Trajectories Derived from Research Literature: Sequence, Repetition, Conditionals. In
Proceedings of the 2017 ACM Conference on International Computing Education Research (pp. 182-190). Tacoma, Washington, USA. doi:10.1145/3105726.3106166
Sung, W., Ahn, J., & Black, J. B. (2017). Introducing computational thinking to young
learners: Practicing computational perspectives through embodiment in mathematics
education. Technology, Knowledge and Learning, 22(3), 443-463. doi:
Tatar, D., Harrison, S., Stewart, M. Frisina, C. & Musaeus, P. (2017). Proto-computational
thinking: The uncomfortable underpinnings. In P. J. Rich & C. B. Hodges (Eds.) Emerging Research, Practice, and Policy on Computational Thinking (pp.63 – 84). Springer International Publishing
Trninic, D. (2018). Instruction, repetition, discovery: restoring the historical educational role of
practice. Instructional Science, 46(1), 133–153. https://doi.org/10.1007/s11251-017-9443-z
Whitehead, A. N. (1967). The aims of education. Available at
https://archive.org/details/AlfredNorthWhiteheadAimsOfEducation1967
Short Abstract
A research informed dialogue exploring the affordances of a wooden puzzle game, Archelino, for scaffolding understanding of the process of decomposition as used in computational thinking and computational disposition in the early years. Suggestions for adaptations to classroom and home use are offered.
Funding
The work in this paper was enabled by a University of Alberta New Faculty Startup grant.
About
Steven Khan is Assistant Professor, Mathematics Education and Computational Thinking at the University of Alberta, Edmonton.
Sally Rudakoff. is Lead Teacher, Numeracy and Education Technology for St. Albert Public Schools and a member of the Alberta Teachers’ Association.