By:  Diane Hobenshield Tepylo & Lisa Floyd

Lisa taught Computational Thinking in Math and Science Courses at Western University’s Faculty of Education in the recent Winter Term. She also teaches high school computer science and math with the Thames Valley District School Board in London, Ontario. She is a passionate advocate for getting young kids to code. She is currently a grad student pursing her Masters of Professional Education in the field of mathematics and likes to research new ways to enhance understanding of math concepts for young people. As a mother of three young sons, she appreciates toys that make learning fun yet challenging. Follow her on Twitter @lisaannefloyd

Recently there has been substantial interest in teaching coding throughout the K-12 curriculum as there are numerous educational benefits (cf. Kafai and Burke 2014; Resnick et al. 2009).  Coding develops computational thinking – skills such as problem solving, pattern recognition, problem decomposition and abstraction to create models, algorithm design, and the analysis and visualization of data (Wing 2006). There are increasing efforts to promote coding as a means for teaching mathematics (Gadanidis 2015; Misfeldt and Ejsing-Dunn 2015), specifically in elementary students (Papert 1980, 1993, 1994).

As secondary mathematics and programming teachers, we have learned that there is great potential to use programming to teach mathematics concepts. When we began teaching programming, we taught the content in a sequential manner. We presented lessons introducing specific commands, expressions, and constructs, followed by a series of exercises to practice those structures. Occasionally we assigned a problem that we thought would require students to consolidate the taught structures. Some students succeeded with this approach, but many needed substantial help to solve the problem. We had demonstrated the tools, but had not helped the students understand the mathematics behind their use.

Driven to help our students be more successful, we independently experimented in our individual classrooms, expanding our teaching repertoires. Listening to how our students understood the programing commands and structures, we adjusted our teaching to help our students become better at programming. By doing so, we found that our students were learning mathematics.

Here, we share several examples of mathematical learning through programming: improving student understanding of division and place value.

Division, Remainders And Rounding In Context

Many students struggle with making sense of remainders in context (Carpenter et al. 1983; E.A. Silver 1997; E. A. Silver et al. 1993). For example with the question, “an army bus holds 36 soldiers. If 1128 soldiers are being bused to their training site, how many buses are needed?” (Carpenter et al. 1983). A significant number of students spit out the result 31.333 or 31 1/3 for the bus problem without considering what the fractional portion means. Can there be 1/3 of a bus?  Alternatively, many students follow the learned rule, ‘if the fraction is less than half, round down.’ This rule results in an answer of 31 buses.  Students do not consider how the remaining 12 solders (1/3 of 36) will be transported. Li and Silver (2000) argue that once students have learned about fractions and decimals, students follow algorithms with no consideration about what the fractional portion of the answer means in the context of the problem.

In computer science courses, different programming commands act as tools that help focus attention on meaningful use of remainders. In many programming languages, there are three types of division: regular, integer and modulus – in Python these are written   ‘/’ for regular division, ‘//’ to determine the integer portion of a division and ‘%’ for modulus division, which returns the remainder. As we introduce these programming statements, we facilitate discussions with our students about the different uses of these commands, making references to mathematics and real-life problems.

We did not always include this discussion. When we began teaching computer science, we just taught the commands and expected the students to use them appropriately.  Some students could, but many students struggled to identify when they would use the different types of division. Hypothesizing that these students needed to better understand division with remainders, we both independently decided that we had to teach the mathematical aspects of division and remainders to meet our programming goals. The resulting mathematical discussion is often animated. We see “eureka” instances as students first understand and then generate examples of contexts requiring each type of division based on how the remainder will be used.

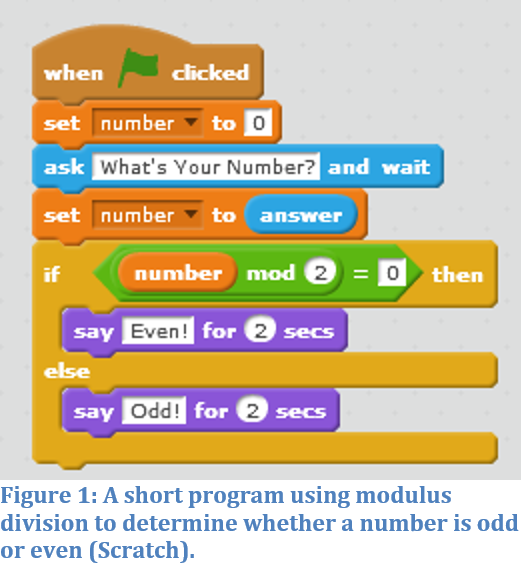
For example, the teacher might raise the problem of having the computer decide whether a number is odd or even.  The students usually will say that even numbers are divisible by two.  We then reframe this as, “What does ‘divisible by two’ mean?” We focus their attention on remainders and the options we have in the programming language.  With this discussion, the students come to realize that “divisible by two” means there is a remainder of zero when the number is divided by two; thus they can use modulus division, %. After this discussion, the class might then outline the logic of the program in pseudo-code before the students work to make the computer solve this problem. Figures 1 and 2 show typical student solutions in Scratch and Python respectively.

 

Place Value

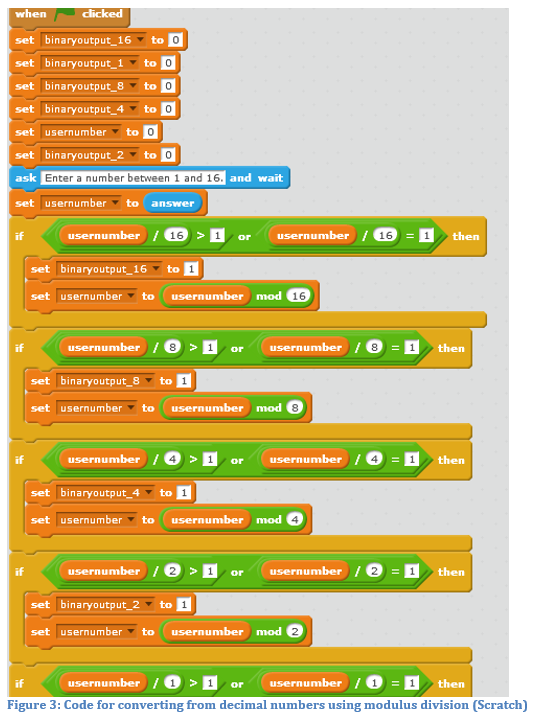
The modulus division command is used in another important number sense concept – place value – in the context of binary numbers.

We begin teaching binary by using chairs to physically count students (unplugged). The first student sits in the first chair, representing the “ones” position. When a second student arrives at a chair, the class discusses how to regroup and the importance of the place value of each chair.

We then extend this unplugged activity to simulate converting a decimal number to binary. The students decide what is the greatest place value that the chairs can represent. For example with decimal 5, one student sits in the ‘4’ chair, representing four students. The class then decides how to represent the remaining one student (five students minus the four represented). There are not enough students for the ‘2’ chair, so that chair remains empty.  The one remaining students sits in the ‘1’ chair.’  This process is repeated with different decimal numbers until the students understand regrouping and binary place value.  Only when the students understand, do we then start discussing how to program the computer to do this conversion using modulus division (see figure 3). Research suggests that comparing different place value systems builds a stronger understanding of place value (Zazkis and Truman 2015).

A more challenging question requiring remainders is the “Donut-hole” question from CS Circles (CEMC Universtiy of Waterloo 2010). In this problem, the programmer has to write a program that determines the most price-effective way to purchase mini-donuts for a party (the donut-holes come in three sized boxes). The class first discusses several cases of this problem using specific numbers, discussing how the integer result and the remainder result are used to determine the number of each box size that is needed. The class then works to build an abstraction of these concrete cases, sometimes acting out the decisions. Once the students have an understanding of what is happening in the problem, small groups write up the logic of the problem (pseudo-code) before the students code the solution individually or in pairs.

After helping the students understand the three different division commands through discussion and collaboratively using these tools in meaningful context, we provide other challenges to help students consolidate their understanding of remainders in context. We create challenges to help students to extend their understanding of integer and modulus division such as writing programs to:

• Determine the best buy on fertilizer for submitted yards and field dimensions
• Convert decimal numbers to binary format
• Create their own system of money where denominations are not based on multiples of ten, and create a program that converts between units (figure 4)
• Create a program for base 5 or base 16 (hexadecimal)

The three types of division address some issues with remainders, but not the issue of inappropriate rounding that is routinely observed for questions like the bus problem. When students obtain a fractional answer, they have learned to round down when the fractional portion is less than half and round up when it is above half. In the bus question, 36 1/3 is rounded down to 36, leaving 12 soldiers without a bus. We often see this type of mindless rule following in the first weeks of our programming courses. For example, Diane has had a student passionately argue that $7.37 needs to be rounded to $7.00, because 37 cents is less than half of a dollar.

Again, different commands within a programming language provide a framework for sense-making about rounding. Many programming languages have three commands for rounding: one to round down to the next integer (math.floor in Python), one to round up, (math.ceil in Python) and one for traditional rounding to a specific decimal place—round (ndigits). For the students, the fact that programming languages provide three different rounding commands confers legitimacy to our argument that there is more than one way to round. Each different command becomes a tool for thinking about different rounding strategies and what makes sense in the context of a problem.

The three division commands and the three rounding commands do not exist in isolation from each other. They are all related to making sense of division problems and some result in the answer.  For example integer division (4//3) and math.floor (4/3) produce the same result, 1.  We help students see these connections by having them solve a challenge without using a specific command and by having the students program a solution to the same problem in more than one language.  Some programming languages, especially introductory languages, do not include every programming command found in more sophisticated languages. For example, Scratch does not have integer division but students soon realize that rounding with the floor command produces the same result. We find these activities help our students make connections between division and rounding commands.

Teacher Moves that Lead to Math Learning in Programming

Using the three types of division commands to discuss the meanings of remainders in context is just one example of mathematical learning in programming classes. This mathematical learning does not automatically happen through programming. We have found that rich problems are important as is making the mathematics explicit.

Rich Engaging Problems in a Variety of Contexts

Choosing a variety of rich, engaging problem contexts is important to build mathematics through programming. By selecting contexts that engage students, students attend to lessons and persevere in solving problems such as converting Vrobits. Even when working with more abstract problems, we try to give students some choice in the problems. We find these contexts and choice keep our students interested and persistent when the concepts become difficult (Middleton & Jansen, 2011).

We also plan problems that require students to create a need for the mathematics. We provide contexts like games that require variables, and data types, and problems such as the bus remainder and ‘Donut-Hole’ problems where we know the students will struggle, and then as they get frustrated, provide programming tools to help them solve their problem. These tools become more meaningful when students need and seek out the tool. We discuss the mathematics behind specific programming commands within the problem context. In the context of division, we often teach the different division commands when the students are struggling with a problem that cannot be solved without them.

Making the Mathematics Explicit

When helping students to solve rich problems, we explicitly focus the students’ attention on the mathematic concepts within in the programming commands. With the three different types of division commands, we discuss where each command might be used and have the students generate situations where each command is appropriate. We use the code as “objects to think with” (Papert 1980, 1993; Hoyles & Noss 2015; Moore-Russo et al. 2015). With practice, the students turn the commands into instruments for thinking about other problems.

In addition to the explicit way we use specific coding commands, we also use the explicitness of programming to help development mathematical understanding. We help students develop this explicitness through class discussions, developing and refining the pseudo-code in small groups and whole group settings. Pseudo-code, because it is in English, makes the mathematics explicit, without having to worry about learning new symbols. The students then, individually or in pairs, convert this pseudo-code plan into code and run their proposed solution. The computer immediately gives feedback as to whether the mathematical abstraction is correct. After all, “the best and worst thing about computers is that the computer will do exactly what you tell it to do” (Guttag 2013, p 4).

This pseudo-code, code, test cycle also helps students move through levels of abstractness (Ke, 2014).  Progression from concrete, to representations to abstract symbols is thought to help students learn (Bruner 1966). In our classes, we start discussing specific concrete mathematical problems, and then represent the problem solution in pseudo-code, before writing the solution in code. In running the code, the code again becomes concrete. The proposed solution in code is then further refined – with the students’ thinking represented verbally and in writing.

Moving forward – What we have learned

From our classroom experiences, our students seemed to better understand mathematics concepts such as number sense after learning different programming commands. By using rich problems, where students require specific programming commands that are mathematical in nature; and by explicitly discussing the mathematics inherent to the programming commands, our students improve their understanding of the mathematics and programming concepts. Our experiences suggests there is great potential for mathematics learning in coding: teachers must plan for the mathematics to be visible to students for mathematical learning to occur.

---

References

Bruner, J. S., Oliver, R. R., & Greenfield, P. M. (1966). Studies in cognitive growth. New York: Wiley.

Carpenter, T. P., Lindquist, M., Matthews, W., & Silver, E. A. (1983). Results of the Third NAEP Mathematics Assessment: Secondary School. Mathematics Teacher, 76(9), 652-659.

CEMC Universtiy of Waterloo (2010). 6D: Design, Debugging and Donuts. http://cscircles.cemc.uwaterloo.ca/6d-design/.

Gadanidis, G. (2015). Coding as a trojan horse for mathematics reform. Journal of Computers in Mathematics and Science Teaching (2015) 34(2), 155-173, 34(2), 155-173.

Guttag, J. V. (2013). Introduction to Computation and Programming Using Python. Cambridge, MA: MIT Press.

Kafai, Y., & Burke, Q. (2014). Connected code: Why chldren need to learn pragrammming. MIT Press: Cambridge, MA.

Li, Y., & Silver, E. A. (2000). Can younger students succeed where older students fail? An examination of third graders’ solutions of a division-with-remainder (DWR) problem. Journal of Mathematical Behavior, 19(2), 233-246.

Misfeldt, M., & Ejsing-Dunn, S. (2015). Learning mathematics through programming: An instrumental approach to potentials and pitfalls. Paper presented at the CERME 9, Prague, CZ,

Papert, S. (1980, 1993). Mindstorms: Children, computers, and powerful ideas. Second Edition. New York, NY: Basic Books.

Papert, S. (1994). The children’s machine: Rethinking school in the age of the computer. New York, NY: Basic Books.

Resnick, M., Maloney, J., Monroy-Hernández, A., Rusk, N., Eastmond, E., Brennan, K., et al. (2009). Scratch: Programming for all. Communications of the ACM, 52(11), 60-67.

Silver, E. A. (1997). Algebra for all: Increasing students’ access to algebraic ideas, not just algebra courses. Mathematics Teaching in the Middle School, 2(4), 204-207.

Silver, E. A., Shapiro, L. J., & A., D. (1993). Sense making and the solution of division problems involving remainders: An examination of middle school students’ solution processes and their interpretations of solutions. Journal for Research in Mathematics Education, 24(2), 117-135.

Zazkis, R., & Truman, J. (2015). From trigonometry to number theory… and back: Extending LCM to rational numbers. Digital Expereinces in Mathematics Education, 1, 79-86.